Discussion Overview
The discussion revolves around the challenge of dividing a domed ceiling into equal pie-shaped sections for the purpose of creating a mural template. Participants explore the geometric considerations involved in accurately representing the curved surface of the dome, which is 14 feet in diameter and 2 feet high at the center.
Discussion Character
- Exploratory
- Technical explanation
- Conceptual clarification
- Debate/contested
- Mathematical reasoning
Main Points Raised
- One participant expresses confusion about how to divide the dome into 6 or 8 equal sections and seeks assistance in determining the shape and size of each piece.
- Another participant suggests that if the dome is spherical, a flat piece of paper cannot conform perfectly to it, recommending experimentation with smaller spheres for approximation.
- A different viewpoint argues that while a flat piece of paper can be cut into curved shapes, it will not perfectly fit the dome's surface, and a formula is needed to determine these shapes.
- Participants discuss the implications of the dome's dimensions, noting that it cannot be a perfect sphere due to its height and diameter, which complicates the geometry involved.
- One participant proposes that the pieces will have straight edges, leading to a discussion about the geometric properties of triangles formed by cutting the dome.
- Another participant suggests that to create a template, one must consider the arc measurements and the width of the bottom of each section, indicating a preference for fewer sections to maintain simplicity.
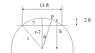
- A later reply provides a geometric approach to finding the radius and dimensions of the template, using trigonometric relationships and Pythagorean theorem to derive necessary measurements.
- One participant expresses gratitude for the provided geometric insights, indicating that they were helpful in understanding the problem.
- Another participant introduces the concept of using a dymaxion map to simplify the dome's surface into a polyhedron, suggesting it as a potential solution for transferring the design.
Areas of Agreement / Disagreement
Participants exhibit a range of views on the feasibility of laying flat templates on a curved surface, with some believing it is possible while others argue against it. There is no consensus on the best method to achieve the desired outcome, and multiple competing approaches are discussed.
Contextual Notes
Participants mention various assumptions about the dome's shape and dimensions, which may affect the calculations and proposed methods. The discussion includes unresolved mathematical steps and dependencies on specific geometric definitions.