momogiri
- 52
- 0
Water flows steadily from an open tank as in the figure below. The elevation of point 1 is 10.0m, and the elevation of points 2 and 3 is 2.00m. The cross-sectional area at point 2 is 0.0480m^2; at point 3 it is 0.0160m^2. The area of the tank is very large compared with the cross-sectional area of the pipe.
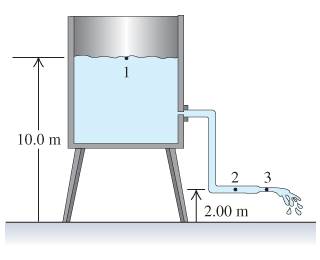
Part A is "Assuming that Bernoulli's equation applies, compute the discharge rate in cubic meters per second."
Which I've solved using Bernoulli's principle
so Q_3 = 0.200m^3/s
Part B is "What is the gauge pressure at point 2?"
Now this one I'm stuck with, but here's what I've done:
A_2*v_2 = A_3*v_3
(0.048)v_2 = (0.2)(0.016)
v_2 = 0.0666667m/s
so using Bernoulli's principle..(and cancelling some stuff)
P_2 + 0.5*rho*v_2^2 = P_3 + 0.5*rho*v_3^2
which becomes
P_2 + (0.5)(1000)(0.0666667)^2 = 101300 + (0.5)(1000)(0.2)^2
thus P_2 = 101317.7778
And I figured since gauge pressure meant P_G = P - atm
I subtracted 101317.7778 by 101300
which got me 17.7778 as my gauge pressure...
So what am I doing wrong? I don't seem to be getting the right answer here...
Part A is "Assuming that Bernoulli's equation applies, compute the discharge rate in cubic meters per second."
Which I've solved using Bernoulli's principle
so Q_3 = 0.200m^3/s
Part B is "What is the gauge pressure at point 2?"
Now this one I'm stuck with, but here's what I've done:
A_2*v_2 = A_3*v_3
(0.048)v_2 = (0.2)(0.016)
v_2 = 0.0666667m/s
so using Bernoulli's principle..(and cancelling some stuff)
P_2 + 0.5*rho*v_2^2 = P_3 + 0.5*rho*v_3^2
which becomes
P_2 + (0.5)(1000)(0.0666667)^2 = 101300 + (0.5)(1000)(0.2)^2
thus P_2 = 101317.7778
And I figured since gauge pressure meant P_G = P - atm
I subtracted 101317.7778 by 101300
which got me 17.7778 as my gauge pressure...
So what am I doing wrong? I don't seem to be getting the right answer here...