How Does the ss¯ Pair Affect the Partial Width Γ2 in Gluon Decays?

  • #1
VikasRajG
3
0
TL;DR Summary
How to calculate/estimate partial decay width of a decay when gluons decaying to a quark-antiquark pair are involved?
How do we normally calculate the partial width Γi for a decay involving gluons.Consider the following example:

feynmanbjks.png
feynmareal.png

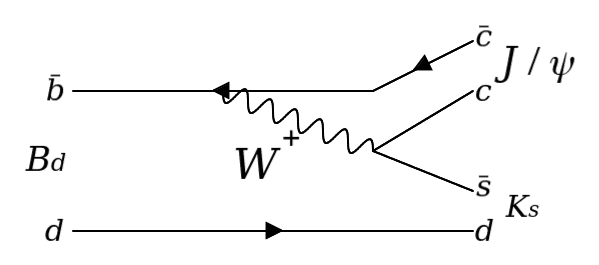
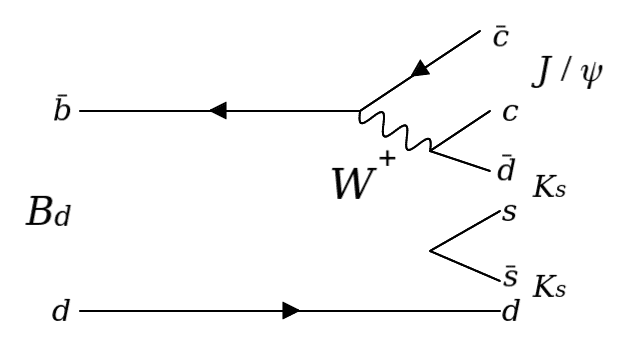
in the first example, I know that one can estimate the partial width Γ1 using CKM matrix elements to get "Γ1 is directly proportional to V2cb V2cs
."Now, for the second diagram it is essentially the same but with an additive gluon going to ss¯¯¯

. Ofcourse, the partial width now changes to look like:
"Γ2 is directly proportional to V2cb V2cd
."BUT,this doesn't tell anything on how the gluon changes things. So what I want to know is, how exactly does the ss¯¯¯

pair changing the Γ2
!!!????If there are any sources/articles for this, it would be really helpful as I haven't found much regarding these 3 body decays!
 
Physics news on Phys.org
  • #2
What are you looking for exactly? Someone to calculate the matrix element for you?
 
  • #3
Have you even read the whole thing?
I know how to calculate the CKM matrix element, I am asking how to consider the gluon to ssbar contribution in decay width!
 
  • #4
VikasRajG said:
Have you even read the whole thing?
In am not your servant. Don't treat me like one.

You put a propagator in for the gluon, and T matrices at each colored vertex.
 
  • #5
Thank You!
Sorry for that, I was just a bit frustrated.
 

FAQ: How Does the ss¯ Pair Affect the Partial Width Γ2 in Gluon Decays?

What is the ss¯ pair in the context of gluon decays?

In the context of gluon decays, the ss¯ pair refers to a strange quark (s) and its corresponding antiquark (s¯). These pairs can be produced in the process of gluon fragmentation or decay, and their presence can influence the properties and outcomes of these decays.

How does the presence of an ss¯ pair influence the partial width Γ2 in gluon decays?

The presence of an ss¯ pair can affect the partial width Γ2 in gluon decays by providing an additional decay channel. This can lead to an increase in the partial width Γ2, as the gluon can decay into final states that include the ss¯ pair, thereby modifying the overall decay dynamics and branching ratios.

Why is it important to study the effect of ss¯ pairs on gluon decay widths?

Studying the effect of ss¯ pairs on gluon decay widths is important because it helps improve our understanding of quantum chromodynamics (QCD), the theory describing the strong interaction. By analyzing these effects, scientists can make more accurate predictions about particle interactions and decay processes, which are crucial for experiments in high-energy physics.

What methods are used to calculate the impact of ss¯ pairs on partial widths in gluon decays?

To calculate the impact of ss¯ pairs on partial widths in gluon decays, theoretical physicists use perturbative QCD techniques, Feynman diagrams, and lattice QCD simulations. These methods allow for precise calculations of decay amplitudes and widths by taking into account the contributions from ss¯ pairs and other possible quark-antiquark pairs.

Can experimental data confirm the theoretical predictions about ss¯ pairs and partial widths in gluon decays?

Yes, experimental data can confirm the theoretical predictions about ss¯ pairs and partial widths in gluon decays. High-energy physics experiments, such as those conducted at particle colliders like the Large Hadron Collider (LHC), provide data on gluon decay processes. By comparing this data with theoretical predictions, scientists can validate their models and refine their understanding of QCD and particle interactions.

Similar threads

I How often would a ϕ meson decay to a electron-positron pair?
Replies
2
Views
2K
How Does the Mass of the Bottom Quark Affect Z Boson Decay Calculations?
Replies
6
Views
4K
I How do the collider experiments measure the mass of the W boson?
Replies
4
Views
3K
Particle Physics: Partial Decay Widths and Branching Ratios
Replies
5
Views
9K
I B -> s µµ decays: Current status
2
Replies
49
Views
10K
Calculating Decay Widths & Estimating Partial Width of τ− Lepton
Replies
1
Views
3K
How Does Detector Resolution Affect the True Width of the J/psi Particle?
Replies
2
Views
4K
I How does the raster scan frequency affect the accuracy of a CRT TV picture?
Replies
32
Views
3K
B Decays affected by all new particles/fields?
Replies
18
Views
3K
How Does Diffusion Affect the Decay Chain of Uranium?
Replies
1
Views
1K

Hot Threads

Recent Insights

Back
Top