How is the Equation Derived for an Isosceles Triangle with a specific Angle?

[anemone]

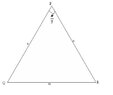
Given a triangle $PQR$ where $QR=m$, $PQ=PR=n$ and $\angle P=\dfrac{\pi}{7}$.

View attachment 2522

Show that $m^4-3m^2n^2-mn^3+n^4=0$.

 

[Opalg]

[sp]Half the angle at $P$ is $\dfrac{\pi}{14}$. The triangle is isosceles, so it follows that $\sin\Bigl(\dfrac\pi{14}\Bigr) = \dfrac{m/2}n = \dfrac m{2n}.$

If $\theta = \frac\pi{14}$ then $\sin(7\theta) = 1.$ But if $s = \sin\theta$ then $\sin(7\theta) = 7s - 56s^3 + 112s^5 - 64s^7$ (using the Chebyshev polynomial $T_7(s)$). So the equation $\sin(7\theta) = 1$ can be written as $64s^7 - 112s^5 + 56s^3 - 7s + 1 = 0$. That can be factored as $$\begin{aligned} 0 &= 64s^7 - 112s^5 + 56s^3 - 7s + 1\\ &= (s+1)(64s^6 - 64s^5 - 48s^4 + 48s^3 + 8s^2 - 8s + 1) \\ &= (s+1)(8s^3 - 4s^2 - 4s + 1)^2.\end{aligned}$$ So if $\sin(7\theta) = 1$ but $s\ne-1$ then $8s^3 - 4s^2 - 4s + 1 = 0.$

Now put $s = \sin\bigl(\frac\pi{14}\bigr) = \frac m{2n}$ to see that $$ 0 = 8s^3 - 4s^2 - 4s + 1 = \frac{8m^3}{8n^3} - \frac{4m^2}{4n^2} - \frac{4m}{2n} + 1 = \frac{m^3 - m^2n - 2mn^2 + n^3}{n^3},$$ and therefore $m^3 - m^2n - 2mn^2 + n^3 = 0.$ Finally, multiply that by $m+n$ to see that $0 = (m+n)(m^3 - m^2n - 2mn^2 + n^3) = m^4 - 3m^2n^2 - mn^3 + n^4.$[/sp]

 

[anemone]

[sp]Half the angle at $P$ is $\dfrac{\pi}{14}$. The triangle is isosceles, so it follows that $\sin\Bigl(\dfrac\pi{14}\Bigr) = \dfrac{m/2}n = \dfrac m{2n}.$

If $\theta = \frac\pi{14}$ then $\sin(7\theta) = 1.$ But if $s = \sin\theta$ then $\sin(7\theta) = 7s - 56s^3 + 112s^5 - 64s^7$ (using the Chebyshev polynomial $T_7(s)$). So the equation $\sin(7\theta) = 1$ can be written as $64s^7 - 112s^5 + 56s^3 - 7s + 1 = 0$. That can be factored as $$\begin{aligned} 0 &= 64s^7 - 112s^5 + 56s^3 - 7s + 1\\ &= (s+1)(64s^6 - 64s^5 - 48s^4 + 48s^3 + 8s^2 - 8s + 1) \\ &= (s+1)(8s^3 - 4s^2 - 4s + 1)^2.\end{aligned}$$ So if $\sin(7\theta) = 1$ but $s\ne-1$ then $8s^3 - 4s^2 - 4s + 1 = 0.$

Now put $s = \sin\bigl(\frac\pi{14}\bigr) = \frac m{2n}$ to see that $$ 0 = 8s^3 - 4s^2 - 4s + 1 = \frac{8m^3}{8n^3} - \frac{4m^2}{4n^2} - \frac{4m}{2n} + 1 = \frac{m^3 - m^2n - 2mn^2 + n^3}{n^3},$$ and therefore $m^3 - m^2n - 2mn^2 + n^3 = 0.$ Finally, multiply that by $m+n$ to see that $0 = (m+n)(m^3 - m^2n - 2mn^2 + n^3) = m^4 - 3m^2n^2 - mn^3 + n^4.$[/sp]

What a beautiful solution it is, Mr. Opalg! (Sun)(Clapping)

My solution:

Spoiler

My solution used the "identity" that states $\cos \dfrac{\pi}{7}+\cos \dfrac{3\pi}{7}+\cos \dfrac{5\pi}{7}=\dfrac{1}{2}$.

By applying the Cosine Rule to the triangle $PQR$, we get:

$\cos \dfrac{\pi}{7}=\dfrac{2n^2-m^2}{2n^2}$,

$\cos \dfrac{3\pi}{7}=\dfrac{m}{2n}$ and finally,

$\cos \dfrac{5\pi}{7}=\cos \left( \pi-\dfrac{2\pi}{7} \right)=-\cos \dfrac{2\pi}{7}=-\left( 2\cos^2 \dfrac{\pi}{7}-1 \right)=1-2\left(\dfrac{2n^2-m^2}{2n^2} \right)^2$

Now, by adding these three we get:

$\dfrac{2n^2-m^2}{2n^2}+\dfrac{m}{2n}+1-2\left(\dfrac{2n^2-m^2}{2n^2} \right)^2=\dfrac{1}{2}$

and simplifying these we get:

$m^4-3m^2n^2-mn^3+n^4=0$

But I'm not sure if I have to show how does one get the identity of $\cos \dfrac{\pi}{7}+\cos \dfrac{3\pi}{7}+\cos \dfrac{5\pi}{7}=\dfrac{1}{2}$ before using it or it's a well-known identity that one can just refer to it when needed...