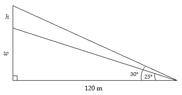
Discussion Overview
The discussion revolves around calculating the height of a flagpole using trigonometric principles, specifically through the application of angles of elevation from a fixed horizontal distance. The context includes both diagrammatic representation and mathematical reasoning related to the problem.
Discussion Character
- Mathematical reasoning
- Technical explanation
- Homework-related
Main Points Raised
- One participant presents the problem setup, including angles of elevation and horizontal distance, and attempts to draw a diagram.
- Another participant suggests using tangent functions to express the relationships between the height of the flagpole and the angles of elevation, proposing to eliminate one variable using another equation.
- A different participant reiterates the tangent relationships and provides a calculation for the height of the flagpole, arriving at a value of approximately 13.33 meters.
- Another participant reformulates the equations to express the height in terms of the tangent of the angles, confirming the height calculation while emphasizing the importance of avoiding intermediary rounding to maintain accuracy.
- There is a discussion about the relative sizes of the angles of elevation, with a participant noting that the angle corresponding to the higher point must be greater.
Areas of Agreement / Disagreement
Participants generally agree on the approach to solving the problem using trigonometric functions, and some calculations align closely. However, there is no explicit consensus on the method of rounding or the best practices for accuracy in calculations.
Contextual Notes
Some participants express uncertainty about the accuracy of their calculations and the implications of rounding during the problem-solving process. There are also assumptions regarding the relationships between the angles and the heights that are not fully explored.
Who May Find This Useful
Students or individuals interested in applying trigonometry to real-world problems, particularly in geometry and physics contexts, may find this discussion beneficial.