How many transmitters are needed to secure a 3x4 castle arrangement?

[bio]

Well, I, as the King of the World, have built the great Tower of Me! However, because everyone seems to hate me for some reason, citizens keep trying to enter my tower to kill me. So, I have assigned some laser transmitters in my castle. However, as the technology is new, a laser transmitter can only cover the edge of one tower. An edge of a tower is protected by having at least one transmitter at the end of its vertices. This is my castle at the moment:

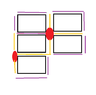
View attachment 8101Black rectangles represent towers. Red dots represent transmitters. Orange lines represent laser-protected edges. Purple lines represent unprotected edges.

However, I have been faced with a few problems:

a) My adviser thinks I can protect the castle with only 5 transmitters. I understand that a transmitter will have to protect at least 3 edges, but how can this be done?

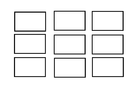
Good News! My castle now has 9 towers, in a 3*3 arrangement!

View attachment 8102

b) After working with my advisers for many hours, we found we couldn't use just 5 transmitters to cover this up. So, how do we protect it with 6?

c) However, is 6 really the minimum amount of transmitters needed? Could we use less?

Greater News! My castle is now in a 3*4 arrangement, with 3 new towers!

View attachment 8103

d) However, we've only got 8 more transmitters. So, is it possible to cover this whole area up, and how? If we can't cover them all, what is the maximum amount of towers that can be protected?

Please answer there questions in a 9th-10th grade intelligence level, as I don't understand some concepts in maths.

(Sorry for my bad drawings)

EDIT: In the first drawing, the line extending left from the top transmitter should be coloured in as protected.

 

[mrtwhs]

This sounds like a variant of the Art Gallery Theorem. Try googling "Art Gallery Theorem".

 

[bio]

This sounds like a variant of the Art Gallery Theorem. Try googling "Art Gallery Theorem".

Yes, however AGT is for simple polygons, and the eyesight of the guard can stretch indefinitely. My polygon is irregular, and the laser is limited to the length of one tower

 

[mrtwhs]

This sounds like a variant of the Art Gallery Theorem. Try googling "Art Gallery Theorem" ... and then look for a variant where guards have limited range. Also, simple and irregular are not opposites of one another.

If you model each picture as a graph with edges along the towers and vertices between the towers then your pictures become a $$4 \times 3$$ grid graph with the lower right two edges missing. The other two pictures are $$4 \times 4$$ and $$4 \times 5$$ grid graphs.

Your first picture can be done with 5, the second with 8 and the third with 10. I have no idea if these are minimal.

 

[Opalg]

For part a), you can place the transmitters like this:
[TIKZ][scale=0.75]
\clip (-0.75,-0.75) rectangle (7.75,8.75) ;
\def\laser#1{\node at (#1) [circle,fill=red] {} ; \draw[ultra thick, orange] (#1) +(-3.5cm,-0cm) -- +(-0.3cm,0cm) +(0.3cm,0cm) -- +(3.5cm,0cm) +(0cm,0.3cm) -- +(0cm,2.5cm) +(0cm,-0.3cm) -- +(0cm,-2.5cm) }
\foreach \point in {(0,0),(0,3),(4,3),(0,6),(4,6)}
\draw[ultra thick] \point rectangle +(3,2) ;
\coordinate (A) at (3.5,8.5) ;
\coordinate (B) at (-0.5,5.5) ;
\coordinate (C) at (7.5,5.5) ;
\coordinate (D) at (3.5,2.5) ;
\coordinate (E) at (-0.5,-0.5) ;
\foreach \point in {A,B,C,D,E}
\laser{\point};[/TIKZ]

For part b), it cannot be done with six transmitters. As mrtwhs has said, you need eight, as for example in this layout:

[TIKZ][scale=0.75]
\clip (-0.75,-0.75) rectangle (11.75,8.75) ;
\def\laser#1{\node at (#1) [circle,fill=red] {} ; \draw[ultra thick, orange] (#1) +(-3.5cm,-0cm) -- +(-0.3cm,0cm) +(0.3cm,0cm) -- +(3.5cm,0cm) +(0cm,0.3cm) -- +(0cm,2.5cm) +(0cm,-0.3cm) -- +(0cm,-2.5cm) }
\foreach \point in {(0,0),(0,3),(0,6),(4,0),(4,3),(4,6),(8,0),(8,3),(8,6)}
\draw[ultra thick] \point rectangle +(3,2) ;
\coordinate (A) at (3.5,8.5) ;
\coordinate (B) at (-0.5,5.5) ;
\coordinate (C) at (7.5,5.5) ;
\coordinate (D) at (3.5,2.5) ;
\coordinate (E) at (-0.5,-0.5) ;
\coordinate (F) at (7.5,-0.5) ;
\coordinate (G) at (11.5,2.5) ;
\coordinate (H) at (11.5,8.5) ;
\foreach \point in {A,B,C,D,E,F,G,H}
\laser{\point};
\foreach \point in {C,D}
\fill [black,opacity=0.25] (\point) circle (0.25cm) ;
\foreach \point in {(3.5,5.5),(7.5,2.5)}
\fill [green] \point circle (0.15cm) ;[/TIKZ]

To see that it cannot be done with fewer than eight transmitters, count the number of edges that need to be covered. The nine rectangles have a total of 36 edges, of which 12 are external and 24 are internal. The 24 internal edges are arranged in 12 pairs of facing edges, and each such pair can be covered by a single laser beam. So we need enough transmitters to be able to cover 12+12 = 24 different directions.

A transmitter can cover a maximum of four different directions. But there are only at most two locations where a transmitter can cover all four directions without overlapping other transmitters. (In the above diagram, the two locations indicated by darker red dots cover four directions each. There are two other possible locations for this, indicated by the small green dots. But transmitters placed there would overlap with the edges already covered from the dark red locations.)

Suppose that you only have seven transmitters. Two of them can cover four directions each, but the remaining five can only cover at most three new directions each. So the total number of directions covered by all seven transmitters is at most $2\times 4 + 5\times3 = 8 + 15 = 23$. That is not enough to cover all 24 directions required. Therefore at least eight transmitters are needed for the $3\times3$ arrangement of towers.

It looks to me as though this problem should have had a $3\times2$ arrangement of towers for part b), and a $3\times3$ arrangement for part c). Then the minimal number of transmitters would be 6 for b) and 8 for c), as stated in the problem.

 

[bio]

For part a), you can place the transmitters like this:
[TIKZ][scale=0.75]
\clip (-0.75,-0.75) rectangle (7.75,8.75) ;
\def\laser#1{\node at (#1) [circle,fill=red] {} ; \draw[ultra thick, orange] (#1) +(-3.5cm,-0cm) -- +(-0.3cm,0cm) +(0.3cm,0cm) -- +(3.5cm,0cm) +(0cm,0.3cm) -- +(0cm,2.5cm) +(0cm,-0.3cm) -- +(0cm,-2.5cm) }
\foreach \point in {(0,0),(0,3),(4,3),(0,6),(4,6)}
\draw[ultra thick] \point rectangle +(3,2) ;
\coordinate (A) at (3.5,8.5) ;
\coordinate (B) at (-0.5,5.5) ;
\coordinate (C) at (7.5,5.5) ;
\coordinate (D) at (3.5,2.5) ;
\coordinate (E) at (-0.5,-0.5) ;
\foreach \point in {A,B,C,D,E}
\laser{\point};[/TIKZ]

For part b), it cannot be done with six transmitters. As mrtwhs has said, you need eight, as for example in this layout:

[TIKZ][scale=0.75]
\clip (-0.75,-0.75) rectangle (11.75,8.75) ;
\def\laser#1{\node at (#1) [circle,fill=red] {} ; \draw[ultra thick, orange] (#1) +(-3.5cm,-0cm) -- +(-0.3cm,0cm) +(0.3cm,0cm) -- +(3.5cm,0cm) +(0cm,0.3cm) -- +(0cm,2.5cm) +(0cm,-0.3cm) -- +(0cm,-2.5cm) }
\foreach \point in {(0,0),(0,3),(0,6),(4,0),(4,3),(4,6),(8,0),(8,3),(8,6)}
\draw[ultra thick] \point rectangle +(3,2) ;
\coordinate (A) at (3.5,8.5) ;
\coordinate (B) at (-0.5,5.5) ;
\coordinate (C) at (7.5,5.5) ;
\coordinate (D) at (3.5,2.5) ;
\coordinate (E) at (-0.5,-0.5) ;
\coordinate (F) at (7.5,-0.5) ;
\coordinate (G) at (11.5,2.5) ;
\coordinate (H) at (11.5,8.5) ;
\foreach \point in {A,B,C,D,E,F,G,H}
\laser{\point};
\foreach \point in {C,D}
\fill [black,opacity=0.25] (\point) circle (0.25cm) ;
\foreach \point in {(3.5,5.5),(7.5,2.5)}
\fill [green] \point circle (0.15cm) ;[/TIKZ]

To see that it cannot be done with fewer than eight transmitters, count the number of edges that need to be covered. The nine rectangles have a total of 36 edges, of which 12 are external and 24 are internal. The 24 internal edges are arranged in 12 pairs of facing edges, and each such pair can be covered by a single laser beam. So we need enough transmitters to be able to cover 12+12 = 24 different directions.

A transmitter can cover a maximum of four different directions. But there are only at most two locations where a transmitter can cover all four directions without overlapping other transmitters. (In the above diagram, the two locations indicated by darker red dots cover four directions each. There are two other possible locations for this, indicated by the small green dots. But transmitters placed there would overlap with the edges already covered from the dark red locations.)

Suppose that you only have seven transmitters. Two of them can cover four directions each, but the remaining five can only cover at most three new directions each. So the total number of directions covered by all seven transmitters is at most $2\times 4 + 5\times3 = 8 + 15 = 23$. That is not enough to cover all 24 directions required. Therefore at least eight transmitters are needed for the $3\times3$ arrangement of towers.

It looks to me as though this problem should have had a $3\times2$ arrangement of towers for part b), and a $3\times3$ arrangement for part c). Then the minimal number of transmitters would be 6 for b) and 8 for c), as stated in the problem.

Thank you, however how can you do it with question d)? And what if, for the 3*3 castle, I only protected the outer boundary?

 

[mrtwhs]

Opalg's picture shows that you can guard the outside of what you are calling the 3x3 castle with 6 transmitters.

As for part d), I answered that earlier. I think it is 10.