How Tall Are Indonesians Compared to Dutchmen?

[mathmari]

Hey!

I am looking at the following:

The average tallest men live in Netherlands and Montenegro mit $1.83$m=$183$cm.
The average shortest men live in Indonesia mit $1.58$m=$158$cm.
The standard deviation of the height in Netherlands/Montenegro is $9.7$cm and in Indonesia it is $7.8$cm.

The height of a giant of Indonesia is exactly 2 standard deviations over the average height of an Indonesian. He goes to Netherlands. Which is the part of the Netherlands that are taller than that giant?

I thought to do the following:

Since the height of a giant of Indonesia is exactly 2 standard deviations over the average height of an Indonesian, we get that his height is $158+2\cdot 7.8=173.6$cm, right?

We have the following:
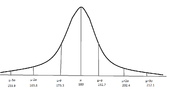
View attachment 6314

Now we want to compute $P(x>173.6)=1-P(x\leq 173.6)$, right? (Wondering)
At the graph we have $173.3$ how could we compute the $P(x\leq 173.6)$ ? (Wondering)

 

[Jameson]

Hi mathmari,

I'm still waking up so forgive any errors in thought.

Your logic looks sound to me. The height of the giant from Indonesia is 173.6, and the question is what percent of the population in the Netherlands is taller than this?

So from here it just depends on the method you're expected to use. I work with statistics quite a bit and a program like R or even Wolfram Alpha will easily tell you that probability, but in general there are 4 ways I can think of:

1) Use a software package to output the probability.
2) Use the definition of the normal distribution and approximate this area by approximating an integral.
3) Standardize this distribution to a Normal(0,1) distribution, then look up the value in a table (very old method).
4) Use the fact that 2 SD above the mean for Indonesia is very close to one SD below the the mean for the Netherlands ($183-9.7 = 173.3$). If we use this as approximately 173.6 then we can use the empirical rule to estimate the probability.

It all depends on the expectation of the question. Which method do you think is most appropriate? In practice, (1) is definitely what we would do.

 

[mathmari]

Hi mathmari,

I'm still waking up so forgive any errors in thought.

Your logic looks sound to me. The height of the giant from Indonesia is 173.6, and the question is what percent of the population in the Netherlands is taller than this?

So from here it just depends on the method you're expected to use. I work with statistics quite a bit and a program like R or even Wolfram Alpha will easily tell you that probability, but in general there are 4 ways I can think of:

1) Use a software package to output the probability.
2) Use the definition of the normal distribution and approximate this area by approximating an integral.
3) Standardize this distribution to a Normal(0,1) distribution, then look up the value in a table (very old method).
4) Use the fact that 2 SD above the mean for Indonesia is very close to one SD below the the mean for the Netherlands ($183-9.7 = 173.3$). If we use this as approximately 173.6 then we can use the empirical rule to estimate the probability.

It all depends on the expectation of the question. Which method do you think is most appropriate? In practice, (1) is definitely what we would do.

Let's use (4):

From the graph we have that $P(x\leq 173.3)=50\%-\frac{68\%}{2}=16\%$, or not? (Wondering)

So, we have that $P(x>173.3)=1-P(x\leq 173.3)=1-0.16=0.84$.

Does this mean that appoximately $84$% of the Netherlands are taller than the giant? (Wondering)

 

[Jameson]

That looks like a reasonable approximation to me. Again, my apologies if later on today I come back and say otherwise. I'm heading out the door and half asleep.

Here is the exact area from R:

> 1-pnorm(173.6,183,9.7)
          [1] 0.8337454

 

[I like Serena]

Heh. I'm from the Netherlands.
Almost every man I know, and most women as well, are considered Indonesian giants! ;)
And the men that are not giants typically have origins outside of the Netherlands.
As it is, I'm just shy of being a giant myself. (Doh)

 

[mathmari]

Ah ok!

Then to be in the Indonesian basketaball team one has to be at the one percent tallest of the country. Which is the minimum height that someone has to have to be in the team?

Let $m$ be the minimal acceptable height, then $P(x\geq m)=0,01$, or not? (Wondering)
But how can we compute $m$, again from the graph of the Indonesian, this time? (Wondering)

Is the Netherlands would have the same minimal height, how many would have height bigger than $m$ ? (Wondering)

 

[I like Serena]

Ah ok!

Then to be in the Indonesian basketaball team one has to be at the one percent tallest of the country. Which is the minimum height that someone has to have to be in the team?

Let $m$ be the minimal acceptable height, then $P(x\geq m)=0,01$, or not? (Wondering)
But how can we compute $m$, again from the graph of the Indonesian, this time? (Wondering)

Is the Netherlands would have the same minimal height, how many would have height bigger than $m$ ? (Wondering)

Suppose we pick an online calculator or table and look up which z-score corresponds to a cumulative probability of 0.01 (or even better: 0.99)? (Wondering)

That z-score is the number of standard deviations above (or below) the mean that we need.

First hit I get from google is for instance: Normal Distribution Calculator

 

[mathmari]

Suppose we pick an online calculator or table and look up which z-score corresponds to a cumulative probability of 0.01 (or even better: 0.99)? (Wondering)

That z-score is the number of standard deviations above (or below) the mean that we need.

First hit I get from google is for instance: Normal Distribution Calculator

From this calculator we get that $P(x\leq 176.146)=0.99$. That means that $1-P(X>176.146)=0.01$, right? (Wondering)

So, we have to use a calculator in this case, or would be also possible without? (Wondering) For the last question, we want to calculate $P(X>176.146)$ for the Netherlands. Using again that calculator we get $P(X\leq 176.146)=0.23991 \Rightarrow 1-P(X\leq 176.146)=1-0.23991 \Rightarrow P(X>176.146)=0.76009$.

Is this correct? (Wondering)

 

[mathmari]

Could we maybe show this also using standardized radom variable? (Wondering)

 

[mathmari]

I have done the following: $$P(X>m)=0,01 \Rightarrow 1-P(X>m)=1-0,01 \Rightarrow P(X\leq m)=0.99 \Rightarrow \Phi \left (\frac{m-158}{7.8}\right )=0.99$$

From the table we get $\frac{m-158}{7.8}=2.32 \Rightarrow m=176.174\ cm$. Is this correct? For the second question: $$P(X>176)=1-P(X\leq 176)=1-\Phi \left (\frac{176-183}{9.7}\right )\cong 1-\Phi (-0.72) \Rightarrow P(X>176)=1-0.23576=0.76424$$ Is this correct?

 

[I like Serena]

Hey mathmari! (Smile)

It seems to me you're asking for confirmation for something you already know.

Oh well, all right, yes, what you're writing is all correct! (Nod)

 

[mathmari]

It seems to me you're asking for confirmation for something you already know.

Oh well, all right, yes, what you're writing is all correct! (Nod)

Thank you! (Mmm)