B How To Consistently Explain Electromagnetism With Relativity

[jartsa]

Okay, thanks for all the responses. I've figured out that in the first situation, all forces cancel except for the magnetic attraction between the two moving electrons. But in the second situation, I'm still working on it. The two protons in each wire repel each other electrostatically, but also attract magnetically, right? But since electrostatic force is stronger than magnetic, this would mean there's a net repulsion yet this is not true so I must be wrong somewhere.

Well now the two positive thighs at the top right corner of the picture attract the one negative thing at the bottom right corner of the picture. Just normal electrostatic attraction. Oh yes, the two positive things would be farther apart if they we not moving.If we make the positive things move together very fast, we can ignore net force between them, because the net force becomes very small. If the fast motion causes more positive things to get into the picture ... then it isn't so simple.

 

[Geocentricist]

In what setup, in what frame, between what objects?

In the frame of two wires with moving electrons, if a moving electron repels another moving electron with an electrostatic force of 1 then how strong is the magnetic attraction between them?

Well now the two positive thighs at the top right corner of the picture attract the one negative thing at the bottom right corner of the picture. Just normal electrostatic attraction.

Okay, but doesn't the top proton pair repel the bottom proton pair with double the force that it attracts the bottom electron? So the top wire is still, overall, repelling the bottom wire, contrary to the result I'm aiming for (the reality that the two wires attract).

Also I wanted to bump one of the original questions I had in the OP about Veritasium's video, which is, are they mistaken in portraying the electron-frame electron spacing different at different times?

 

[jartsa]

Okay, but doesn't the top proton pair repel the bottom proton pair with double the force that it attracts the bottom electron? So the top wire is still, overall, repelling the bottom wire, contrary to the result I'm aiming for (the reality that the two wires attract).

No. There's the 'magnetism' thing. Parallel currents attract.

But now that I thought about it I noticed that the contraction thing and the 'magnetism' thing cancel out in the electron frame. No matter how fast the protons move the net force between them is the always the same - which means it's the same as when the speed is zero. This is in the electron frame.

 

[Geocentricist]

No. There's the 'magnetism' thing. Parallel currents attract.

I know that if I put two wires with identical current side-by-side they will attract. But I want to know why this is by understanding the electrostatic and magnetic forces between the protons and electrons. That's why I'm confused as to how they can attract given they are both net positive (they each have 2 protons per electron). So there must be some magnetic force that overcomes this repulsion. Since the electrons aren't moving, they can have nothing to do with this magnetic force as it only involves moving charges. So does the magnetic attraction between two co-moving pairs of protons overcome their mutual electrostatic repulsion?

But now that I thought about it I noticed that the contraction thing and the 'magnetism' thing cancel out in the electron frame. No matter how fast the protons move the net force between them is the always the same - which means it's the same as when the speed is zero. This is in the electron frame.

I'm confused. When the protons don't move there's only one proton in the wire as opposed to two. So how could the net force between them be the same?

 

[jartsa]

I'm confused. When the protons don't move there's only one proton in the wire as opposed to two. So how could the net force between them be the same?

No motion - no contraction.
No motion - no 'magnetism'.

 

[jartsa]

I know that if I put two wires with identical current side-by-side they will attract. But I want to know why this is by understanding the electrostatic and magnetic forces between the protons and electrons. That's why I'm confused as to how they can attract given they are both net positive (they each have 2 protons per electron). So there must be some magnetic force that overcomes this repulsion. Since the electrons aren't moving, they can have nothing to do with this magnetic force as it only involves moving charges. So does the magnetic attraction between two co-moving pairs of protons overcome their mutual electrostatic repulsion?

Well that sounds correct - it's just that contraction causes complications.

An electron sees a contracted proton formation and is strongly attracted to that. That's the reason why the wires attract. That's the reason in the electron frame.

A proton sees a normal density of electrons, and protons. Protons repulse protons normally, electrons attract protons normally. But electrons repel electrons with smaller force than normally, because of 'magnetism'. That's the reason the wires attract, in the proton frame.

 

[jartsa]

Also I wanted to bump one of the original questions I had in the OP about Veritasium's video, which is, are they mistaken in portraying the electron-frame electron spacing different at different times?

They are correct.

And now I notice that I ignored that effect in the previous post.

 

[Dale]

Since the electrons aren't moving, they can have nothing to do with this magnetic force as it only involves moving charges.

But they do reduce the electrostatic repulsion substantially. In fact they reduce the electrostatic repulsion so that it is smaller than the magnetic attraction. You cannot neglect the electrons the way you are trying to.

So does the magnetic attraction between two co-moving pairs of protons overcome their mutual electrostatic repulsion?

No, it does not. But a wire is more than just protons.

 

[Geocentricist]

An electron sees a contracted proton formation and is strongly attracted to that. That's the reason why the wires attract. That's the reason in the electron frame.

This seems overly simplistic to me. Of course I don't mean you're wrong, but I don't understand how that can be correct. Sure, the top electron is attracted to the two protons it sees in the other wire. That's 2 units of attraction. But this electron is not far-sighted, so it must also see the two protons in its own wire, and conclude that these two protons both repulse the two protons in the other wire. That's 4 units of repulsion (top proton A repulses both bottom protons, and top proton B also repulses both bottom protons). So how do you explain that?

A proton sees a normal density of electrons, and protons. Protons repulse protons normally, electrons attract protons normally. But electrons repel electrons with smaller force than normally, because of 'magnetism'. That's the reason the wires attract, in the proton frame.

I understand the proton frame

 

[pervect]

[QUOTE="Geocentricist, post: 5886958, member: 636108"
Veritasium's Video On Electromagnetism

I'm referring to this video:

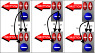
Notice the separation in the electrons' rest frame at 1:17. Twelve electrons fit on the screen.

At 1:28 the electrons start moving but their separation remains the same.

At 2:08 the electrons' rest frame is again shown but the separation has increased so only 8 of them fit on the screen, and no explanation is provided for why this is.

Did Veritasium make a mistake with this video?

Another thing is at 1:28 when the electrons start moving, it seems their density should increase, and attract the cat-ion. Yet this density increase is not shown. In fact the narrator specifically says the density doesn't change.

I've posted all these questions to Reddit but response time is very, very slow there.[/QUOTE]
[/quote]

The video is basically an adaptation of Purcell's approach to electromagnetism. I believe this is form his book "Electricity and Magnetism", https://www.amazon.com/dp/1107014026/?tag=pfamazon01-20, but I don't own that book so my impulse to look it up and make sure my memory is correct on the title will have to go unsatisfied.

Purcell's explanation is correct, but causes a lot of confusion. The thing people typically get confused about is more or less what you're confused about. That is the fact that a wire that is neutral in the lab frame stays neutral in the lab frame when you start a current flowing through it.

Because of this difficulty, I don't recommend Purcell's approach, though it is correct and in the literature. The two approaches I'd suggest are learning Maxwell's equations, or learning the four-vector treatment of special relativity.

About all I can say about why the wire stays neutral in the lab frame is that it is a consequence of the conservation of electric charge (which is formalized by Maxwell's equations). If the total charge of the wire + battery is zero before you hook the battery up to the wire and start the current flowing, the total charge remains zero after you connect the battery, though the charges do move.

This argument doesn't show why the charges stay uniformly distributed throughout the wire, though, but it does demonstrate that the total charge must remain zero.

Note that this seems to be contradicted by the video, when the wire picks up a positive charge in the "cat frame". But when one includes the fact that a wire carying a current does not exist in isolation, one realizes there must be another wire with a return path that's not shown on the diagram, and the charge on that wire that is not shown balances out the charge picked up by the wire that is shown.

This extra complication makes Purcell's approach rather unsatisfying. It avoid using the Lorentz transform of special relativity, but in my opinion that's it's downfall. The Lorentz transform contains an additional effect besides length contraction and time dilation. This effect is the relativity of simultaneity. Without this missing piece, the length contraction and time dilation expanations are not complete. The mathematical treatment using the Lorentz transform is complete, but it's not a pretty picture like the ones you have been drawing.

I have to run - I hope this helps some.

 

[Geocentricist]

They are correct.

They are correct that electron spacing changes in the electron rest-frame? Why would the electrons move further apart from each other? They haven't done anything. There's no cause for them to separate.

 

[Geocentricist]

Purcell's explanation is correct, but causes a lot of confusion. The thing people typically get confused about is more or less what you're confused about. That is the fact that a wire that is neutral in the lab frame stays neutral in the lab frame when you start a current flowing through it.

That's only one problem for me, but I can get over it by just accepting electron spacing doesn't contract when they move.

Because of this difficulty, I don't recommend Purcell's approach, though it is correct and in the literature. The two approaches I'd suggest are learning Maxwell's equations, or learning the four-vector treatment of special relativity.

I'm trying to understand the phenomena to the point where I can illustrate it graphically. I don't think Maxwell's equations or four-vector treatment is a shortcut to that goal, but rather a detour. I'm a visual person and I avoid math whenever possible. I'm not aware of any compelling reason why this phenomena can't be illustrated graphically and only mathematically.

Note that this seems to be contradicted by the video, when the wire picks up a positive charge in the "cat frame". But when one includes the fact that a wire carying a current does not exist in isolation, one realizes there must be another wire with a return path that's not shown on the diagram, and the charge on that wire that is not shown balances out the charge picked up by the wire that is shown.

This part actually doesn't bother me

The mathematical treatment using the Lorentz transform is complete, but it's not a pretty picture like the ones you have been drawing.

Surely there's nothing preventing me from illustrating the two frames graphically? Even if the protons and electrons aren't discrete particles (for whatever reason) that doesn't stop me from illustrating them as probability clouds, or whatever.

Thanks for your time.

 

[pervect]

Surely there's nothing preventing me from illustrating the two frames graphically? Even if the protons and electrons aren't discrete particles (for whatever reason) that doesn't stop me from illustrating them as probability clouds, or whatever.

Thanks for your time.

The video is from my brief inspection, correct. You can check it vs Purcell's textbook, or with online web resources (http://physics.weber.edu/schroeder/mrr/MRRtalk.html comes to mind), though of course it's much better to check it against the original source. Some web pages are correct and useful - others, not so much, and then there are the ones that are completely wrong and misleading.

Some of the "field line" approaches briefly mentioned in the article I linked to might be useful. They are very visual, though, and one can correctly get the electric part of the field of a moving charge simply by Lorentz-contracting the field lines.

You'll find plenty of illustrations of field lines if you look - the direction of the field lines gives the direction of the force, the density of the lines gives the magnitude of the force.

http://www.feynmanlectures.caltech.edu/img/FLP_II/f26-04/f26-04_tc_big.svgz

http://www.feynmanlectures.caltech.edu/img/FLP_II/f26-05/f26-05_tc_big.svgz

For example, the above, the field lines of a single charge taken from one of Feynman's lectures. Above are the electric field lines, one of a stationary charge, directly below it are the electric field lines of a moving charge. Below that is one of the magnetic field lines of a moving charge. You'll need to include the forces due to both the magnetic and electric fields to get the total force. The rules for interpreting electric field line diagram are that the field lines point in the direction of the force, and the density of the field lines gives the magnitude of the force. The rules for magnetic field lines are simila (but not quite the same). The magnetic force on a stationary charge is zero, only moving charges experience a magnetic force.

An explanation of why this approach works get quite deep, but if we avoid explaining why it works, it does seem to meet your visual criterion of a visual presentation.

The above gives the field lines for a single charge (moving and stationary). The field lines add together, but getting a correct diagram for a wire consisting of many charges without use of some of the applicable math (like Gauss' law, in particular) will be challenging. Gauss law isn't particularly hard to master and ties in well with the field line approach.

http://www.physicsclassroom.com/class/estatics/Lesson-4/Electric-Field-Lines also has some further explanations of the field line approach along with spelling out the applicable rules in detail, something I did not do in my short post which is mainly motivational and letting you know the approach exists.

 

[jtbell]

They are correct that electron spacing changes in the electron rest-frame? Why would the electrons move further apart from each other? They haven't done anything. There's no cause for them to separate.

This is just length contraction in reverse. Consider a rod (e.g. a meter-stick) that is stationary in your rest-frame. Now you start to move so that in your new reference rame, the rod is moving parallel to its length. The length of the rod that you measure in this frame is shorter than the length that you measure in your original frame. Why should the rod decrease in length? It hasn't done anything.

You need to come to grips with the true nature of length contraction, which is a space-time geometrical "perspective" effect determined by the relative velocity of the object in question and its observer, not a "physical" effect caused by interactions within the object.

 

[jartsa]

Why would the electrons move further apart from each other? They haven't done anything.

What is the frame of this question?

In the non-inertial frame of an accelerating electron distant things ahead move very fast, distant things include electrons and clock hands. It's because of relativity of simultaneity.

In some inertial frame an accelerating electron's electric field is getting contracted ... if an electron could hold a ruler, we could say the electron's ruler is contracting in this frame. The ruler would fit more easily between the electrons.

 

[Geocentricist]

This is just length contraction in reverse. Consider a rod (e.g. a meter-stick) that is stationary in your rest-frame. Now you start to move so that in your new reference rame, the rod is moving parallel to its length. The length of the rod that you measure in this frame is shorter than the length that you measure in your original frame. Why should the rod decrease in length? It hasn't done anything.

You need to come to grips with the true nature of length contraction, which is a space-time geometrical "perspective" effect determined by the relative velocity of the object in question and its observer, not a "physical" effect caused by interactions within the object.

I don't think you understand what I'm saying. I'm saying in the electron-frame at time A, their spacing is X. Then, still in the electron-frame, at time B the spacing has increased and is bigger than X. Yet the video provides no explanation for why this happens.

To paraphrase that, we are only dealing with one frame the entire time, the electron rest-frame. By definition, the electrons cannot move, so there can be no electron length contraction (again, the electrons are not moving) so why are the electrons moving further apart in their own rest-frame? That's what the video seems to be showing, and that's what I'm asking about.

What is the frame of this question?

The electron rest-frame. The video in the second instance calls it the cat frame but the cat is co-moving with the electrons so they share the same frame.

 

[Geocentricist]

An explanation of why this approach works get quite deep, but if we avoid explaining why it works, it does seem to meet your visual criterion of a visual presentation.

Thanks for your post. Unfortunately, your link uses a flow of positive charges and stationary negative charges. The opposite of my diagram, and the videos, so I fear I'm only going to confuse myself even more by trying to read that. Also, your images didn't work. I hope you can post them again for me to see.

 

[A.T.]

To paraphrase that, we are only dealing with one frame the entire time, the electron rest-frame. By definition, the electrons cannot move, so there can be no electron length contraction (again, the electrons are not moving) so why are the electrons moving further apart in their own rest-frame?

See:
https://en.wikipedia.org/wiki/Bell's_spaceship_paradox
Just replace rockets with electrons.

If you actually attach a frame to an electron, during it's acceleration, you have time running at different rates along the wire in that frame. This effectively delays the electrons in the back, and speeds up the electrons in the front, so their distances increase.

 

[jartsa]

The electron rest-frame. The video in the second instance calls it the cat frame but the cat is co-moving with the electrons so they share the same frame.

So, cat observes the rest density of electrons, it's 3 per cubic nanometer. Then cat calculates the rest density of protons, which means the density of protons in protons frame, it's 4 per cubic nanometer.

Then the cat wants to know a reason for the asymmetry. Well, the reason is in the past, when something happened to the electrons, while nothing happened to the protons. I mean acceleration. See my previous post for some details about the acceleration.

Oh yes, it was a deceleration in the cat frame. The electrons did not decelerate simultaneously in the cat frame, that caused some deformation of the electron formation in the cat frame.

 

[pervect]

Thanks for your post. Unfortunately, your link uses a flow of positive charges and stationary negative charges. The opposite of my diagram, and the videos, so I fear I'm only going to confuse myself even more by trying to read that. Also, your images didn't work. I hope you can post them again for me to see.

I don't understand why it is so hard to flip the sign, but I'd feel silly arguing about how easy it is. I do want to encourage you to do some more research, reading on the topic, taking full advantage of what's available, preferably not just you-tube videos (though those are better than nothing, I guess).

 

[Dale]

I'm saying in the electron-frame at time A, their spacing is X. Then, still in the electron-frame, at time B the spacing has increased and is bigger than X. Yet the video provides no explanation for why this happens.

To paraphrase that, we are only dealing with one frame the entire time, the electron rest-frame.

The electron rest frame you describe here is non inertial. In non inertial frames things happen for no reason other than that the frame is non inertial.

A good example is a centrifugal force. In a rotating reference frame the centrifugal force can be used to explain things, but it has no source or anything. It just is.

Similarly, in your electron frame there is an inertial force, like the centrifugal force, that spreads the electrons apart. That is the reason people generally would not use a non inertial frame without good reason.

Unfortunately, your link uses a flow of positive charges and stationary negative charges. The opposite of my diagram, and the videos, so I fear I'm only going to confuse myself even more by trying to read that.

This is not an acceptable reason to reject a valid reference. The sign choice is completely arbitrary. Electrons being negative and protons being positive is a convention. Nothing in the physics changes if we choose the opposite convention.

 

[A.T.]

Similarly, in your electron frame there is an inertial force, like the centrifugal force, that spreads the electrons apart.

The inertial force in a frame that accelerates along a line is uniform, so it shouldn't spread the electrons out.

But in that frame you also have time running at different rates along the wire. This effectively delays the electrons in the back, and speeds up the electrons in the front, so their distances increase.

 

[Dale]

@Geocentricist I would strongly recommend avoiding non inertial frames for this discussion. It is not a topic that can be treated at a B level. Instead, stick to two separate inertial scenarios: (1) a pair of long straight parallel wires carrying no current and (2) a pair of long straight parallel wires carrying the same current in the same direction. For both, there should be no switching on or off. The current should be steady throughout all time. For (2) there are two important inertial frames, the rest frame of the protons and the rest frame of the electrons. Those frames are inertial and never change.

 

[Geocentricist]

Okay Dale, I will take your advice and forget about the electron spacing issue in the video for now. I understand both scenarios except for the electron frame of the second. I've been told the top electron is attracted to the bottom two protons and this explains why the wires attract. However it seems this ignores the repulsion between the two pairs of protons which is stronger than the previously mentioned attraction. I'm going to look at that link again and see if it clarifies anything for me.

Update: So I've checked out that link but it only explains the attraction between a particle and a wire, not between two wires. I already understand why a lone moving charge is attracted to a wire with current.

 

[Ibix]

The net electrostatic force is repulsive, yes. But the magnetic force is stronger (in this case) and is attractive.

 

[Geocentricist]

The net electrostatic force is repulsive, yes. But the magnetic force is stronger (in this case) and is attractive.

And this is caused by the motion of the pairs of protons, right? The two pairs of protons have a magnetic attraction to each other?

 

[Ibix]

And this is caused by the motion of the pairs of protons, right? The two pairs of protons have a magnetic attraction to each other?

The magnetic field comes from the moving protons in this frame, yes.

 

[Geocentricist]

The magnetic field comes from the moving protons in this frame, yes.

Okay, let me recap.

1A, electric attraction. 1B, electric repulsion, magnetic attraction. 1C, electric repulsion, magnetic attraction.
2A, electric attraction. 2B, electric repulsion, magnetic attraction. 2C, electric repulsion, magnetic attraction.
3A, electric repulsion. 3B, electric attraction. 3C, electric attraction.

Is this correct? Sorry if it's a lot.

 

[Dale]

Is this correct?

Yes

To find the strength of each repulsion or attraction will require some math (Coulombs law, Biot Savart law, Lorentz force law)

 

[jartsa]

I don't think you understand what I'm saying. I'm saying in the electron-frame at time A, their spacing is X. Then, still in the electron-frame, at time B the spacing has increased and is bigger than X. Yet the video provides no explanation for why this happens.

To paraphrase that, we are only dealing with one frame the entire time, the electron rest-frame.

Oh it's simple:

The video changed frames.

(The video's frame was always the electron's rest frame, because electrons changed frames too.)