How to determine Spinor in Feynman diagram

[Markus Kahn]

TL;DR

I'm confused about how to determine, given the definition of the spin 1/2 fields and the photon field, which Spinor belongs where in a Feynman diagram.

Consider Moller scattering, that is $$e^-(\vec p_1, \alpha)+e^-(\vec p_2, \beta) \quad\longrightarrow\quad e^-(\vec q_1, \gamma)+e^-(\vec q_2, \delta),$$
where the $\vec{p}_i,\vec q_i$ label the momenta of the in and outgoing electrons and the greek letter the spin state.

The two relevant Feynman diagrams at second order in $e$ (electric charge) are

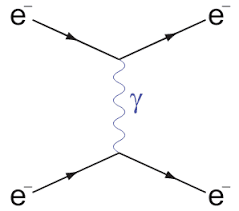
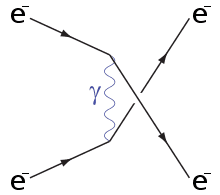
(taken directly from the above linked Wikipedia page)

From QFT we know that we can write the photon and spinor fields as
$$
\begin{align*}
A_\mu(x) &= \int \frac{d^3p}{(2\pi)^32e(\vec p)}[c_a^\dagger(\vec p) {\varepsilon_\mu^a}^*(\vec p)e^{-ip\cdot x} + c_a(\vec p) \varepsilon_\mu^a(\vec p)e^{ip\cdot x}],\\
\psi(x) &= \int \frac{d^3p}{(2\pi)^32e(\vec p)}[a_\alpha^\dagger(\vec p) v_\alpha(\vec{p}) e^{-ip\cdot x} + b_\alpha(\vec p) u_\alpha(\vec p)e^{ip\cdot x}], \\
\bar\psi(x) &= \int \frac{d^3p}{(2\pi)^32e(\vec p)}[a_\alpha(\vec p) \bar v_\alpha(\vec{p}) e^{ip\cdot x} + b_\alpha^\dagger(\vec p) \bar u_\alpha(\vec p)e^{-ip\cdot x}],
\end{align*}
$$
where $a^\dagger$ creates electrons and $b^\dagger$ creates positrons. Note, I'm aware that this deviates from common conventions, but my lecturer wants it that way...

We can now write down the matrix elements of the first Feynman diagram ($t$-channel) using the Feynman rules for QED
$$M_{\alpha\beta\gamma\delta} = \left\{\bar{v}_{\alpha}(\vec p_{1})(-e\gamma^\mu)v_\gamma(\vec q_1)\right\}[-iG_{\mu\nu}(p_1-q_1)] \left\{\bar{v}_\beta (\vec p_2) (-e\gamma^\nu) v_\delta(\vec q_2)\right\}.$$
As I understand it, the expressions in the two curly brackets $\{\hspace{2mm}\}$ are $\mathbb{C}$-numbers, so we could technically swap them without changing the value of the matrix element.

Question
I don't really understand how the expressions in the curly brackets are supposed to be read. Let's take as an example
$$\left\{\bar{v}_{\alpha}(\vec p_{1})(-e\gamma^\mu)v_\gamma(\vec q_1)\right\}.$$
Why do we know that we have to use the spinors $\bar v_\alpha$ and $v_\gamma$ and why not $v_\alpha$ and $\bar v_\gamma$? I do understand that we only need $v_\sigma$ and not $u_\rho$, since we have no positrons, my problem is that I don't really understand the logic when we are supposed to choose the spinor with a bar and when the spinor without a bar.

I tried reading it up in Peskins book, but unfortunately, he just writes it down and says it follows directly from the Feynman rules (see section 5.1, p. 131). I don't really have access to another book at the moment...

 

[Paul Colby]

Isn't it that the electrons on the left are being annihilated while the ones on the right are being created? The conjugation follows from the operator expressions you've provided.

 

[vanhees71]

You have to read Feynman diagrams with Dirac-fermion lines "against" the sense of the arrows on the lines. If this sense of the arrows is the same as the direction of the three-momentum, it's an electron (and you have to use the spinors $u_{\sigma}(\vec{p})$ for the ingoing line and $\bar{u}_{\sigma}(\vec{p})$ for the outgoing. For positrons (the "anti-particles" in QED) the direction of the momenta is opposite to the direction of the arrows on the lines in the Feynman diagarm, and you have to take the spinors $v_{\sigma}(\vec{p})$ for the outgoing positron (whose arrow on the line is going into the vertex!) and $\bar{v}_{\sigma}(\vec{p})$ for the incoming positron (whose arrow on the line pointing out of the verex!).

Now that's why the upper vertex in the first diagram evaluates to something proportional to $\bar{u}_{\sigma_1} (\vec{p}_1) \gamma^{\mu} u_{\sigma_1'}(\vec{q}_1)$. I don't know, why you use $v$'s here, which describe positrons. At the Wikipedia page it's all right, as far as I can see glancing at it.

 

[Markus Kahn]

I don't know, why you use $v$'s here, which describe positrons. At the Wikipedia page it's all right, as far as I can see glancing at it.

Isn't this just a matter of definition? My lecturer demands that we use $v_\alpha$ for electrons (created and annihilated by $a^\dagger$ and $a$) and $u_\alpha$ for positrons (created and annihilated by $b^\dagger$ and $b$), which unfortunately makes looking up stuff sometimes really confusing. Do I understand correctly that in principle I need to switch $v_\alpha(\vec p) \longleftrightarrow u_\alpha (\vec p)$ and $\bar v_\alpha(\vec p) \longleftrightarrow \bar u_\alpha (\vec p)$ in your description to get the right expression for my lecturer's conventions, i.e.
$$
\begin{array}{lll}
\text{incoming} & \text{electron:} & \bar v_\alpha\\
\text{outgoing} & \text{electron:} & v_\alpha\\
\text{incoming} & \text{positorn:} & \bar u_\alpha\\
\text{outgoing} & \text{positron:} & u_\alpha\\
\end{array}
$$

You have to read Feynman diagrams with Dirac-fermion lines "against" the sense of the arrows on the lines. If this sense of the arrows is the same as the direction of the three-momentum, [...]

How do you determine in which direction the three-momentum points?

Isn't it that the electrons on the left are being annihilated while the ones on the right are being created? The conjugation follows from the operator expressions you've provided.

I'm sorry, but I'm not entirely sure what you mean with your comment.

 

[Paul Colby]

I'm sorry, but I'm not entirely sure what you mean with your comment.

Hum, maybe I don't either. $e^{-}(\bar{p}_1,\alpha)$ is annihilated at a vertex. From your expression for $\bar{\psi}$, a factor $\bar{\nu}(p_1)$ multiplies the $a(p_1)$ operator after the integration. Similarly with all the other vertices. What am I missing?

 

[HomogenousCow]

No it's not a matter of definition, there's an LSZ theorem for spinors and the polarization spinors have to be included to project out the asymptotic states that you want. Textbooks usually don't walk you through this because it's cumbersome.

 

[vanhees71]

It's bit confusing, but if your lecturers insist on the opposite naming of the spinors then it must also be changed in the mode decomposition, which then must read
$$\psi(x)=\sum_{\sigma=\pm 1/2} \int_{\mathbb{R}^3} \frac{\mathrm{d}^3 p}{\sqrt{(2 \pi)^2 2 E(\vec{p})}} [v_{\sigma}(\vec{p}) \exp(-\mathrm{i} p \cdot x) \hat{a}_{\sigma} (\vec{p}) + u_{\sigma}(\vec{p}) \exp(+\mathrm{i} p \cdot x) \hat{b}_{\sigma}^{\dagger}(\vec{p})]|_{p^0=E(\vec{p})=\sqrt{m^2+\vec{p}^2}}.$$

On the QED vertex an external electron line with the arrow going in then stands for $v_{\sigma}(\vec{p})$, with an arrow going out for $\bar{v}_{\sigma}(\vec{p})$. The $v$ are notated as a column spinor, then $\bar{v}=v^{\dagger} \gamma^0$ is a row spinor. The diagram at the vertex must be read against the direction of the arrows, i.e., you have $\bar{v}_{\sigma_1}(\vec{p}_1) \gamma^{\mu} v_{\sigma_2}(\vec{p}_2)$, giving a complex number. For electrons the direction of the momenta are in the direction of the arrows: an external electron line with arrow inward depicts an incoming asymptotic free electron; an external electron line with arrow outward depicts an outgoing asymptotic free electron.

For positrons it's everything the same except that the momenta go in the other direction than the arrows in the lines (that's the diagrammatical essence of the Feynman-Stueckelberg trick to interpret the negative-frequency modes as particles with positive energy going in the opposite direction):

an external positron line with arrow inward depicts and outgoing asymptotic free positron; an external positron line with arrow outward depicts an incoming asymptotic free positron.

In my answer above I referred to the convention defined in the Wikipedia article. In your lecturer's convention it's of course all the same, but he labels electron mode functions with $v$ and positron mode functions with $u$.