QED - ordering of Feynman diagram rules

[tomdodd4598]

TL;DR Summary

The ordering of the terms in a Feynman diagram can change its value. Which order is the right one?

Hey there,

In QED, we often have Feynman diagrams involving various numbers of non-commuting components, such as for the one-loop vertex correction (Peskin & Schroeder, page 189):

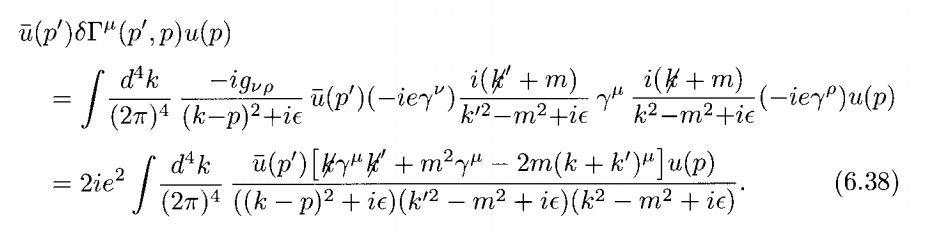
The diagram this integral corresponds to is:

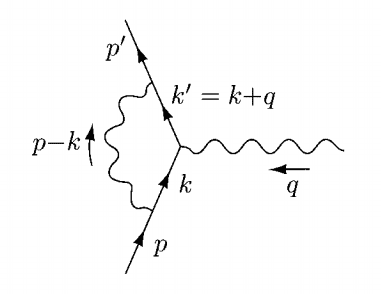
How do we choose which order to put the propagators and vertex factors in? P & S chose this way, but when I tried to work it out before checking with the textbook, I had ${ \gamma }^{ \mu }$ at the front of the expression (corresponding to the vertex at the 'tree-level' position), followed by the ${ k }^{ ' }$ propagator, and looping around counter-clockwise (I used a $k-p$ photon propagator), which led to me being at least a factor of two out, in particular on the term with quadratic numerator.

 

[vanhees71]

The order is implied by the Feynman diagram. In the electron-positron lines you have to read the diagram "against the direction of arrows". For photon lines the direction doesn't matter, because the propagator is symmetric. That's of course, because the electrons/positrons are charged and that's why you have arrows on thir lines which indicate the direction of charge flow while photons are uncharged and thus there's no arrow on their lines.

 

[Gaussian97]

Actually, all the problem with the order comes because of the matrix structure of the Dirac equation, if you have problems with that, I always recommend to write everything in components, then everything commutes and you have no problems, this means to adapt the Feynman rules to be:

• For an incoming electron: $u_a(p)$ where $a$ is a Dirac index.
• For an outgoing electron: $\bar{u}_a(p)$ where $a$ is a Dirac index.
• For the electron propagator: $\frac{i(\not{p}_{ab}+m)}{(p^2-m^2+i\epsilon)}$ where the arrow in the propagator must go from index $b$ to index $a$.
• For the vertex: $-ie\gamma^\mu_{ab}$ where the index $a$ must math the incoming arrow and $b$ the outgoing.

Then, you must sum over Dirac indices that "touch" each other, so the expression in Peskin's Book, could be written as you said
$$\int \frac{d^4 k}{(2\pi)^4} \gamma^\mu_{cd}\frac{i(\not{k}'_{bc}+m)}{(k'^2-m^2+i\epsilon)}\frac{-i g_{\nu\rho}}{(k-p)^2+i\epsilon}\frac{i(\not{k}_{de}+m)}{(k^2-m^2+i\epsilon)}\bar{u}_a(p')u_f(p)(-ie\gamma^\nu_{ab})(-ie\gamma^\rho_{ef})$$
Where repeated index are, of course, summed.
The indices are chosen following

You can see by yourself that, if you want to order the elements in such a way that you can express this sum as a matrix multiplication (remember $(AB)_{ij}=A_{ik}B_{kj}$) you need to order the terms following the fermion line "backwards".
Of course, you must learn to write the correct order without thinking, but while you are learning, you can use this trick in case of doubt.

 

[tomdodd4598]

• For the electron propagator: $\frac{i(\not{p}_{ab}+m)}{(p^2-m^2+i\epsilon)}$ where the arrow in the propagator must go from index $b$ to index $a$.
• For the vertex: $-ie\gamma^\mu_{ab}$ where the index $a$ must math the incoming arrow and $b$ the outgoing.

Ah ha, this is the thing that I didn't know about - thanks! I'm guessing this is apparent when actually determining what the Feynman rules are by starting at the Dyson expansion?

Also, is it that "the index $a$ must math the incoming arrow and $b$ the outgoing" for the vertex $-ie\gamma^\mu_{ab}$, or the other way round? With the former, I get two indices of the same type in the same position - for example, with your diagram labels, I'm getting $\gamma^\mu_{dc}$ rather than $\gamma^\mu_{cd}$.

 

[vanhees71]

As I said, you have to read the Feynman diagrams in the order opposite to the direction of the arrows indicating the current direction. As correctly drawn in #3 in the corresponding vertex the Dirac index $a$ is at the electron-positron leg pointing out of the vertex. As an external line this leg can either mean an outgoing electron ("particle") or an incoming positron ("antiparticle"), depending on which scattering process you want to describe.

On the other vertex it should thus indeed be $\gamma_{cd}^{\mu}$, because $c$ is on the outgoing and $d$ on the incoming leg of the vertex.

 

[Gaussian97]

Also, is it that "the index $a$ must math the incoming arrow and $b$ the outgoing" for the vertex $-ie\gamma^\mu_{ab}$, or the other way round? With the former, I get two indices of the same type in the same position - for example, with your diagram labels, I'm getting $\gamma^\mu_{dc}$ rather than $\gamma^\mu_{cd}$.

Yes, you're right, my mistake, in $-ie\gamma_{ab}$, the index $a$ match the outgoing arrow and the index $b$ match the incoming arrow.

 

[tomdodd4598]

No worries - thanks very much to you both for your detailed help! I grow more and more amazed at how people like Freeman Dyson were able to understand where Feynman’s diagrams came from...