How to determine the wire gauge of thermocouple wires?

[Offline1]

Homework Statement

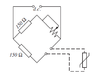
A resistance thermometer bridge circuit shown below has a
designed maximum temperature of 150°C, ignoring the effects of
connecting wire resistance. If the connecting loop is 200 m
determine the smallest gauge (swg) of copper wire which must be
used if the indicated maximum temperature is to be less than 151°C.
The temperature coefficient of resistance of the thermometer is
0.0052 °C–1 and the resistance of the thermometer is 100 at 20°C.
Assume the connecting leads are at 20°C.

Homework Equations

.
[/B]
Rt = R0(1 + at)

R1RT = R2RS

R = pL/A = Resistance = (Resistivity) x Length of wire / cross-sectional area

A = (pi x d2) / 4

d = squareroot(4A /pi)

The Attempt at a Solution

.
[/B]
R0 = Rt /(1 + at)

R0 = 100 /(1 + 0.0052 x 20) = 90.58 ohms

R150 = 90.58 /(1 + 0.0052 x 150) = 50.89 ohms

Fundamental Interval = Rt - R0 = 90.58 - 50.89 = 39.69 ohms = RS

R1RT = R2RS

RT = R2RS / R1 = 150 x 39.69 / 150 = 39.69 ohms

R = pL/A

A = pL/R = (0.0000000168 x 200) / 39.69 = 0.00000336 m2 = 3.36 mm2

d = squareroot(4A /pi) = squareroot(4 x 3.36 / pi) = 4.27mm = 7 swg.

Please let me know if I am in the right direction on this, it's been puzzling me for a few days now!

 

[Tom.G]

Is the temperature coefficient positive or negative?

The temperature coefficient of resistance of the thermometer is
0.0052 °C–1

the resistance of the thermometer is 100 at 20°C

Is this result consistent with your answer to my first question, above?

R150 = 90.58 /(1 + 0.0052 x 150) = 50.89 ohms

So far I've only glanced at your work, there may be other issues lurking there.

 

[Offline1]

I've just noticed that I've put a \ in this formula: RT = R0 x (1 + at), sorry!

 

[Tom.G]

No need to apologize to me, it's your problem. By the way, there are other issues.
How are R1, R2, RS, RT defined, which one is which in the diagram? It's hard to follow your work without knowing what's what.
I suggest you redo 3. The attempt... section with your above modifications, being careful to include all of the terms in the equations when calculating.

Overall, your original post is nicely laid out and easily readable, I wish they all were.

Tom

 

[Offline1]

OK my second attempt.. as for the labelling of the diagram top left is R1, Top right is RS, Bottom left is R2 & Bottom Right is RT.

Rt = R0(1 + at)

R0 = 100 (1 + 0.0052 x 20) = 110.4 ohms

R150 = 110.4(1 + 0.0052 x 150) = 196.5 ohms

Fundamental Interval = Rt - R0 = 196.5 - 110.4 = 86.1 ohms = RS

R1RT = R2RS

RT = R2RS / R1 = 150 x 86.1 / 150 = 86.1 ohms

R = pL/A

A = pL/R = (0.0000000168 x 200) / 86.1 = 0.0000000039 m2 = 0.0039 mm2

d = squareroot(4A /pi) = squareroot(4 x 0.0039/ pi) = 0.07mm = 45 swg

 

[Tom.G]

The temperature coefficient of resistance of the thermometer is
0.0052 °C–1 and the resistance of the thermometer is 100 at 20°C.

Rt = R0(1 + at)

R0 = 100 (1 + 0.0052 x 20) = 110.4 ohms

R150 = 110.4(1 + 0.0052 x 150) = 196.5 ohms

There still seems a bit of trouble with how the sensor resistance varies with temperature. With the temperature coefficient being positive, I have trouble seeing how the resistance can be higher at 0°C than it is at 20°C.

Lets start with Rt, with R_t being the resistance at the working (final) temperature,
R₀ the resistance at the Reference temperature,
T₀ the Reference temperature,
T₁ the working (final) temperature.
α is the temperature coefficient of resistance.

The full formula for this problem at least, is:
R_t = R₀ * ( 1+ α(T₁-T₀))

I can see why you took R0 to be the 0°C resistance, but in engineering the form "T₀" (that is "VARIABLEsub<zero>") is usually taken as the Reference value or Initial value; that is, the value that "VARIABLEsub<something else>" is referred to. Yeah, confusing!

Look up the formula in your textbook; there may be a clearer explanation than the above to help you wrap your brain around it.

And we shall continue.

Tom