How to establish which side of a square a ray will intersect?

[CGandC]

Consider some ray $\bar{r}$ that starts at point $A=(a_x,a_y)$ and faces some direction and consider an upright square ( i.e. it's not rotated ) at some location:

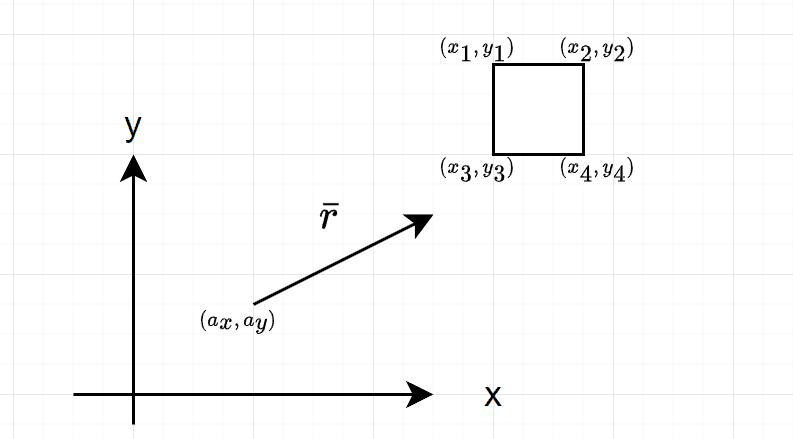Question: if we let the ray continue until hitting the square, how can we detect which face of the square was hit? is there a mathematical equation relating between $\bar{r}$ and the normals of the square that allows me to deduce the intersected face?

I read ( here https://forum.unity.com/threads/how...-a-ray-hit-i-e-raycast-only-backfaces.769556/ ) that checking the ray's direction against the normals of the square can give me the answer but I'm not sure how. ( I know any point on the ray will be of the form $( a_x + \lambda\cdot r_x , a_y + \lambda\cdot r_y )$ for some $\lambda \in \mathbb{R}$ but couldn't reach some useful conclusion with this )

I know there is an algorithmical way of establishing this (based on an algorithm presented here https://permadi.com/1996/05/ray-casting-tutorial-7/ ) and I understand it but I want a more "mathematical" way of establishing which face of the square was hit, an equation perhaps.

 

[phinds]

conceptually trivial, algebraically very messy. You'll need two equations, with the first comparing the slope of the ray to that of the slopes of the lines from (ax,ay) to (x3, y3) and that of the line from (ax,ay) to (x1,y1). That equation will be of a form like X1 < A < X2. If that inequality holds true then the left face gets hit. Then you need a second such equation for the bottom face.

 

[Hill]

Make the equation of your ray in the form $f(x,y)=0$. For any face of the square $(x_a,y_a)(x_b,y_b)$, the ray hits it iff $f(x_a,y_a)f(x_b,y_b)<0$.

 

[CGandC]

conceptually trivial, algebraically very messy. You'll need two equations, with the first comparing the slope of the ray to that of the slopes of the lines from (ax,ay) to (x3, y3) and that of the line from (ax,ay) to (x1,y1). That equation will be of a form like X1 < A < X2. If that inequality holds true then the left face gets hit. Then you need a second such equation for the bottom face.

I understand, thank you so much!

Make the equation of your ray in the form $f(x,y)=0$. For any face of the square $(x_a,y_a)(x_b,y_b)$, the ray hits it iff $f(x_a,y_a)f(x_b,y_b)<0$.

thank you so much, I just a have question regarding this method, I hope you can help me because I want to understand:
The equation of a normal vector $(x,y)$ to the vector $r=(r_x,r_y)$ will be $f(x,y) := x\cdot r_x + y\cdot r_y = 0$, is this the ray equation ( i.e. the $f(x,y)$ ) you were talking about? if it is so, then why multiplying two equations (i.e. $f(x_a,y_a)f(x_b,y_b)<0$ ) of a plane ( straight line in this case since we're at 2D ) will allow me to deduce which face the ray intersected? I just don't understand the correctness of the theorem

 

[Vanadium 50]

Another "conceptually trivial, algebraically very messy."

• Calculate the points of intersection between the sides of the square and the line. Two of these will be on the square (i.e. between the corners)
• Calculate the distance between each of the two points you just calculated and the line's starting point.
• Pick the smallest one.

 

[Hill]

is this the ray equation ( i.e. the f(x,y) ) you were talking about?

No, it is not. What I mean is this. The equation of the line is $y=ax+b$. Make it $y-ax-b=0$. This is the $f(x,y)$.
For any $(x,y)$ on the line, $y-ax-b=0$. For any $(x,y)$ on one side from the line, $y-ax-b>0$. For any $(x,y)$ on the other side, $y-ax-b<0$. The ray intersects a face if the endpoints of the face are on opposite sides from the line, i.e., one has $y-ax-b>0$ and another has $y-ax-b<0$. The product of these two is $<0$ iff the endpoints are on opposite sides from the line.

 

[Ibix]

Given that you know your square's sides are parallel to the axes, just solve for the intercept with the horizontal and vertical lines you get be extending the square's edges seems the simplest approach, no?

 

[CGandC]

Another "conceptually trivial, algebraically very messy."

• Calculate the points of intersection between the sides of the square and the line. Two of these will be on the square (i.e. between the corners)
• Calculate the distance between each of the two points you just calculated and the line's starting point.
• Pick the smallest one.

Very clever indeed. Thank you.

No, it is not. What I mean is this. The equation of the line is $y=ax+b$. Make it $y-ax-b=0$. This is the $f(x,y)$.
For any $(x,y)$ on the line, $y-ax-b=0$. For any $(x,y)$ on one side from the line, $y-ax-b>0$. For any $(x,y)$ on the other side, $y-ax-b<0$. The ray intersects a face if the endpoints of the face are on opposite sides from the line, i.e., one has $y-ax-b>0$ and another has $y-ax-b<0$. The product of these two is $<0$ iff the endpoints are on opposite sides from the line.

I understand perfectly now, very insightful, thank you.

Given that you know your square's sides are parallel to the axes, just solve for the intercept with the horizontal and vertical lines you get be extending the square's edges seems the simplest approach, no?

I agree with you, finding the first point of intersection of the ray with the square and then checking which edge/line it belongs to ( this is done by checking inequalities for different edges similar to those @phinds mentioned ) is the simplest.
In general I wanted to know the different approaches people might take to this problem since I've built my own ray caster in Java and it uses an approach similar to what @Vanadium 50 proposed. I needed to know which face of the square/wall my ray was hitting in the simulation in order to texture them right; after that I thought to myself how would I be able to texturize world objects / arbitrary polygons in a graphics simulation when a ray hits them ( since I'll need to know the face of the polygon the ray had hit ) and the answers here established basis for the answer to this question. Thanks a lot!