How to find out radius by velocity and an angle

[EggEgg]

Homework Statement

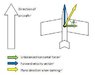
An aircraft remains in flight by generating a force, called Lift, which acts to counter gravity. By design, Lift always acts in the “up” direction of the aircraft frame of reference (i.e., orthogonally to a lateral axis along the wings). An aircraft turns by banking its wings, thereby changing the direction of the Lift force. The diagram to the right illustrates this.
To maintain level flight, the Lift force must increase, so that the vertical component of lift balances gravity. In this situation though there is an unbalanced horizontal turning force, which causes the aircraft to turn in a circle.

Q.1 Determine the lift force, L, required to counter gravity, as a function of the bank angle,\theta

Q.2 Use the above information to determine a function relating the speed of the aircraft and the bank angle to the turning radius (i.e., the radius of the circle inscribed by the aircraft during the turn).

Homework Equations

N/A

The Attempt at a Solution

I have answered Q.1 as:
In bank angle\theta=0, lift force L is equal to gravity g, thus:
(L cos)\theta=g

\theta=cos^-1(g/L)

For Q.2
I know i can use bank angle to find out horizontal force, and use forward velocity with this force to find out the turning angle, but i don't know how to find out the radius with these information

 

[rock.freak667]

The aircraft is turning in a circle, so the resultant of lift and gravity will provide the centripetal force needed to turn in that radius.

So you just need the formula for centripetal force and equate that to the lift-gravity.

 

[EggEgg]

But how about Q2?
i want to know how can i find the radius by a angle \theta
other thing like the lift force, horizontal force and the angle i know how to find it

 

[rock.freak667]

But how about Q2?
i want to know how can i find the radius by a angle \theta
other thing like the lift force, horizontal force and the angle i know how to find it

mv²/r = lift force - gravity

 

[Quinzio]

But how about Q2?
i want to know how can i find the radius by a angle \theta
other thing like the lift force, horizontal force and the angle i know how to find it

Who did the diagram you attached ?
It's very confusing, especially for you that you are trying to solve this problem, and in the end it wrong.

Proceed by steps, and find the force necessary to keep up the plane with a certain bank angle.
Then with the horizontal force, and the speed, you can find the radius.