How to Find the Absolute Min-Max of \(f(x,y)=xy^{2}\) over a Quarter-Circle?

[Yankel]

Hello,

I am trying to find the absolute min-max of the function:

\[f(x,y)=xy^{2}\]

over the set:

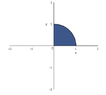
\[D=x^{2}+y^{2}\leq 1, y\geq 0, x\geq 0\]

Usually, when I have a problem where D is a rectangle, I check every line out of 4 for min-max. If D is a triangle, the same. If D is a circle, I usually take the circle line and put it in f in such a way that created a single variable function.

Here, I have a quarter of a circle (photo attached).

View attachment 2599

Now how do I handle it ? I know I need to check the two lines in the region. How do I handle the quarter of a circle ? Should I do:

\[y^{2}=1-x^{2}\]

put it in f, solve and take only points that satisfy x>=0 and y>=0 ?

a better way ?

thanks !

 

[MarkFL]

You may consider the parametrization of $x$ and $y$:

$$x=\cos(t)$$

$$y=\sin(t)$$

Thus, on the boundary, you can write $f$ as a function of the single variable $t$.

 

[Yankel]

Thanks, but I need to solve it by finding critical points, and then looking for all boundary points.

 

[zzephod]

Thanks, but I need to solve it by finding critical points, and then looking for all boundary points.

Your function obviously has its global extrema on the boundary, so there is no need to look for calculus type of extrema on the interior of the region. The boundary is $x=\cos(\theta)$ $y=\sin(\theta)$, so as a function of $\theta$ on the boundary is: $f(\theta)=\cos(\theta)(\sin(\theta))^2$.It is this function you need to find the extrema of.

.

 

[MarkFL]

Thanks, but I need to solve it by finding critical points, and then looking for all boundary points.

Yes, and the parametrization I suggested is one way to examine $f$ on the boundary of the region $D$. :D

 

[Yankel]

you guys don't understand what I need to do. I'll show you what I tried, maybe it will give you a better clue. But as to your suggestion, I must NOT use sin or cos ! even if it makes it easier.

Now, I found the partial derivatives, just to get

\[2xy=0\]

and

\[y^{2}=0\]

this yields one point: (0,0)

Now I looked at the circle, I wrote it as:

\[y^{2}=1-x^{2}\]

and created a single variable function:

\[f(x,1-x^{2})=x^{5}-2x^{3}+x\]

I found it's derivative, compared to 0 and found 4 points:

\[x=\pm 1\]

and

\[x=\pm \frac{1}{5}\]

the negative value are not in the region, so that left me with 2 points to check:

\[(1,0)\]

and

\[(\frac{1}{5},\frac{24}{25})\]

In addition, the points that connects the quarter of a circle with the lines need to be checked, and so I also check (1,0) which is already on the list and (0,1)

I got that the max is

\[f(\frac{1}{5},\frac{24}{25})=0.184\]

and the min is 0.

But, this is wrong answer, according to the book, the answer should be:

\[f(\sqrt{\frac{1}{3}},\sqrt{\frac{2}{3}})=0.384\]and I have no idea where these numbers come from !

Now that you see in what technique I must solve this, can you please help me finding what I am doing wrong here ?

Thanks !

 

[MarkFL]

You initially asked only for a better way, and I was simply trying to point you to an alternate method that is probably computationally simpler.

 

[Yankel]

I apologize for the misunderstandings, I meant a better way within the technique I tried to describe. Now that I specified what I did, should I have done it in a different way, I mean, where did the sqrt(1/3) came from ?

 

[zzephod]

you guys don't understand what I need to do. I'll show you what I tried, maybe it will give you a better clue. But as to your suggestion, I must NOT use sin or cos ! even if it makes it easier.

Now, I found the partial derivatives, just to get

\[2xy=0\]

and

\[y^{2}=0\]

this yields one point: (0,0)

Now I looked at the circle, I wrote it as:

\[y^{2}=1-x^{2}\]

and created a single variable function:

\[f(x,1-x^{2})=x^{5}-2x^{3}+x\]

I found it's derivative, compared to 0 and found 4 points:

\[x=\pm 1\]

and

\[x=\pm \frac{1}{5}\]

the negative value are not in the region, so that left me with 2 points to check:

\[(1,0)\]

and

\[(\frac{1}{5},\frac{24}{25})\]

In addition, the points that connects the quarter of a circle with the lines need to be checked, and so I also check (1,0) which is already on the list and (0,1)

I got that the max is

\[f(\frac{1}{5},\frac{24}{25})=0.184\]

and the min is 0.

But, this is wrong answer, according to the book, the answer should be:

\[f(\sqrt{\frac{1}{3}},\sqrt{\frac{2}{3}})=0.384\]and I have no idea where these numbers come from !

Now that you see in what technique I must solve this, can you please help me finding what I am doing wrong here ?

Thanks !

The feasible region for your function on the boundary is $x \in [0,1]$, your roots other than $x=1$ are wrong. You also need to check for extrema on the rays $x=0$, $y=0$ (well you don't as I said previously the global extrema are on $x^2+y^2=1$ .

But worse your function is wrong $xy^2=x(1-x^2)$ not what you have.

Also if you do not post the question as asked, we will answer the question we think you were asked (and I still think switching to polars will answer your question as asked better than this method).

.

.

 

[Yankel]

Thank you, my mistake was indeed in setting the function. Silly mistake.

Thanks !