How to find the depth of immersion of this boat model?

[PrincessIceFall]

So I am trying to find the depth of immersion of this particular boat model, which has curvilinear edges (subparabolic edges) on each side. The figure of the pontoon is shown below

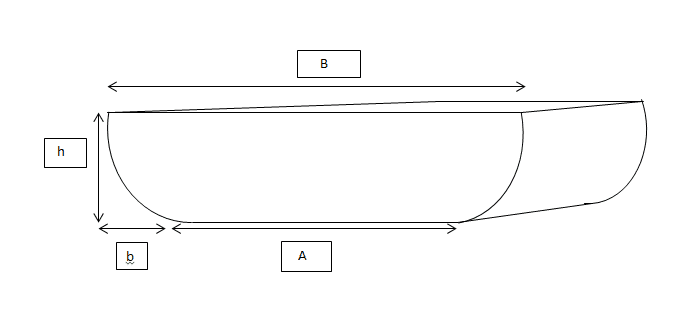
So now when I place this pontoon in water, the height of the water that rises, called the depth of immersion is to be found. I already know how to calculate the displacement volume, but I have no idea how to find the depth of immersion. Below are the steps taken to find the displacement volume

1. Volume of body

I assumed the whole body to be a rectangle and calculated the area of the rectangle first: B*h

And then, since the curves are subparabolic, it is defined by the equation:

y = (h/b^2)*x^2

Integrating the above equation, gives the area under the curve to be:

bh/3

So subtracting : 2*(bh/3) from (B*h) will give the cross sectional area which

C.S.A = (B*h)-(2*(bh/3))

Multiplying this C.S.A with the length of the pontoon (say L) will give the volume

V = (C.S.A)*L = [(B*h)-(2*(bh/3))] * L

So now that volume of the body is known, the following steps are taken to find the displacement volume

2. Density of body

Density = mass of body / Volume

Note: The mass was found by weighing the pontoon on a weighing machine

3. Specific weight of body

Specific weight of body = density of body * g

Note: g = 9.81 m/s^2

4. Weight of body

Weight of body = Specific weight of body * Vbody

5. Weight of water displaced

Weight of displaced water = Specific weight of water * Displaced volume

Note: Specific weight of water = 9810 N/m^3

6. Archimedes principle

According to Archimedes Principle the weight of the body acting downwards is equal to the weight of displaced acting upwards, so

Wbody = 9810 * Vdisp

7. Displaced Volume

And so the displaced volume of water is given by

Vdisp = Wbody/9180

Now another equation for the displacement volume is:

Vdisp = [(B'*h')-(2*(b'h'/3))] * L

h' is the depth of immersion

and B' is the top width at this displaced volume

The problem is that there are two unknowns in the above equation and I just can't figure out how to find the depth of immersion here. If anyone has any idea please please let me know.

 

[SteamKing]

It's not clear from your explanation if you know the weight of the vessel.

In general, in order to find the waterline at which a vessel floats, you need to know the weight (or mass) of the vessel and the location of its center of gravity.

A set of curves which give the displacement, the location of the center of buoyancy, the height of the metacenter, etc., for various drafts (or depths of immersion) can be computed for a vessel hull given its shape. This information is known as the curves of form or hydrostatic curves.

 

[PrincessIceFall]

It's not clear from your explanation if you know the weight of the vessel.

I have infact mentioned that the mass of the body was found by weighing the pontoon on a weighing machine.

 

[SteamKing]

I have infact mentioned that the mass of the body was found by weighing the pontoon on a weighing machine.

You have one of the data items I mentioned then. With only the weight of the vessel known, the best you can hope to achieve is to find the mean draft of the vessel by calculation.

You can also experimentally find the location of the longitudinal and transverse center of gravity of the vessel with it out of the water by trying to balance it on a knife edge or by suspending it from two points and measuring the tension in the lines using a dynamometer. By using this information, the LCG and TCG can be calculated. In order to find VCG, you would need to carry out an inclining experiment.

 

[PrincessIceFall]

In general, in order to find the waterline at which a vessel floats, you need to know the weight (or mass) of the vessel and the location of its center of gravity.

Okay, let's say I do know the location of the centre of gravity. How do you suggest I find the depth of immersion then.

 

[PrincessIceFall]

You have one of the data items I mentioned then. With only the weight of the vessel known, the best you can hope to achieve is to find the mean draft of the vessel by calculation.

Okay, how would I find the mean draft.

 

[SteamKing]

You'll have to assume a draft, make your volume calculation for the hull at that draft, and if the corresponding displacement is different from the weight of the vessel, you'll have to pick a new draft and repeat the calculation. It's a pretty tedious calculation.

Why don't you just put the vessel into some water and measure the draft? The draft can be found a lot quicker than by calculation.

 

[PrincessIceFall]

You'll have to assume a draft, make your volume calculation for the hull at that draft, and if the corresponding displacement is different from the weight of the vessel, you'll have to pick a new draft and repeat the calculation. It's a pretty tedious calculation.

Why don't you just put the vessel into some water and measure the draft? The draft can be found a lot quicker than by calculation.

It is something that I am required to do. Of course I can find the draft through the experiment. But I also need to program theoretical equations.

 

[jack action]

Vdisp = [(B'*h')-(2*(b'h'/3))] * L

[...]

The problem is that there are two unknowns in the above equation

That is not true. The only unknown is h', since:

h' = (h/b^2)*b'^2 --> b' = b*√(h'/h)

B' = A + 2b' = A + 2b*√(h'/h)

So L & Vdisp are known and all others are solely dependent on h', since A, b and h should also be known.

But not easy to isolate h' though:

Vdisp = [(A + 2b*√(h'/h))*h'-2*(b*√(h'/h)h'/3)] * L

Vdisp = [Ah' + √(4b^2/h)*h'^(3/2) - √(4b^2/h)/3*h'^(3/2)] * L

Vdisp/L = Ah' + 2/3*√(4b^2/h) * h'^(3/2)

 

[PrincessIceFall]

That is not true. The only unknown is h', since:

h' = (h/b^2)*b'^2 --> b' = b*√(h'/h)

B' = A + 2b' = A + 2b*√(h'/h)

So L & Vdisp are known and all others are solely dependent on h', since A, b and h should also be known.

But not easy to isolate h' though:

Vdisp = [(A + 2b*√(h'/h))*h'-2*(b*√(h'/h)h'/3)] * L

Vdisp = [Ah' + √(4b^2/h)*h'^(3/2) - √(4b^2/h)/3*h'^(3/2)] * L

Vdisp/L = Ah' + 2/3*√(4b^2/h) * h'^(3/2)

I am going to have to check this myself. But if what you are saying is right then you are my best-est friend in the world.

 

[PrincessIceFall]

I checked it and its correct. And you are right, it is almost impossible to make h' the subject of the formula. One way of doing it is through iterations. Inputting random values of h' until I get the Vdisp I calculated. This could be done through a spreadsheet or plotting a graph.