DrLiangMath
- 21
- 0
AB=3, DC=5, ∠ CAD=$45^o$, AB ⊥ BC. Find the length of AC.
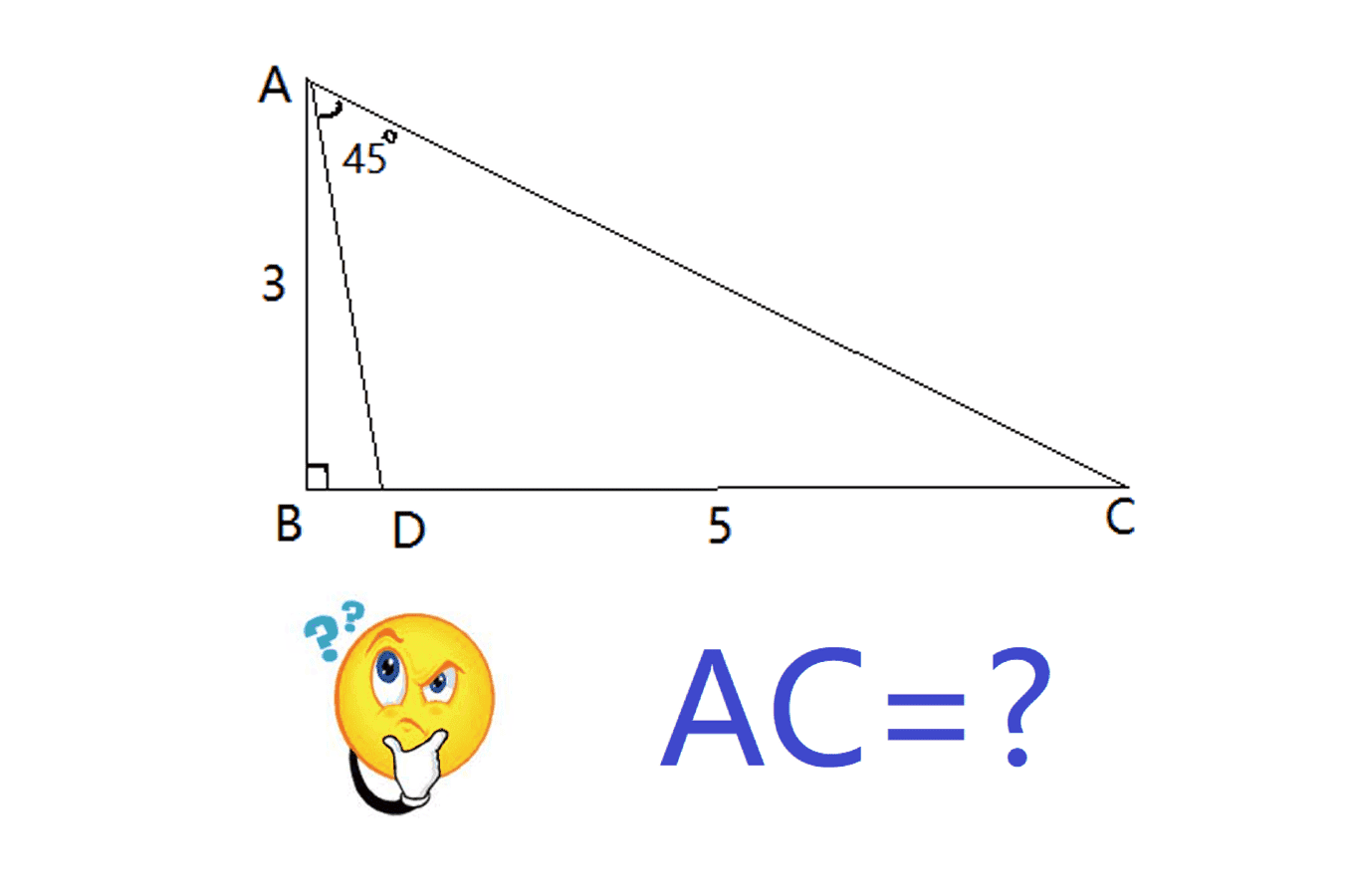
The discussion focuses on calculating the length of the hypotenuse AC in a right triangle where AB=3, DC=5, and angle CAD is 45 degrees. Participants utilize the Law of Sines to derive equations for the triangle, resulting in a biquadratic equation in terms of AC and angle BCA. The conversation highlights the need for an additional equation to solve for two variables, emphasizing the complexity of the problem and the search for a more elegant solution.
PREREQUISITESMathematicians, educators, students studying trigonometry, and anyone interested in geometric problem-solving techniques.
It's inefficient but start by defining angle BCA to be C. Then angle CDA = 135 - C. Call x = AC. Then by Law of SinesMathTutoringByDrLiang said:
I gave two equations. The first is the Law of Sines in triangle ABC and the second is the Law of Sines in triangle ADC. Perhaps I should have stated that.MathTutoringByDrLiang said:Thank you for your response. But we still need one more equation since we have 2 variables x and C.
Klaas van Aarsen said:Hey MathTutoringByDrLiang,
Are you actually looking for an answer to this problem? Or do you have an elegant answer to share?
If the latter, then we might move this thread to the https://mathhelpboards.com/forums/challenge-questions-and-puzzles.28/ subforum.
Btw, at this time I could provide an answer, but it's rather long winded and I'm still looking for a more elegant solution.