SUMMARY
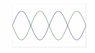
The discussion centers on calculating the wavelength of a transverse wave on a 3-meter long spring oscillating at a frequency of 2.5 Hz. The correct approach involves recognizing that the spring is fixed at both ends and operates in its fourth harmonic. The formula used to determine the wavelength is λ = 2L/n, where L is the length of the spring and n is the harmonic number. Applying this formula yields a wavelength of 1.5 meters, confirming option c) as the correct answer.
PREREQUISITES
- Understanding of harmonic motion and wave properties
- Familiarity with the formula λ = 2L/n for standing waves
- Basic knowledge of frequency and its relationship to wave speed
- Concept of fixed boundary conditions in wave mechanics
NEXT STEPS
- Study the properties of standing waves in fixed strings and springs
- Learn about different harmonics and their mathematical representations
- Explore the relationship between frequency, wavelength, and wave speed in various media
- Investigate practical applications of wave mechanics in musical instruments
USEFUL FOR
Students in physics courses, educators teaching wave mechanics, and anyone interested in understanding the principles of harmonic motion and wave behavior in springs.