vibe3
- 39
- 1
I have two signals (time series) shown in the plot below. Just by looking at the figure, we can see that the two main peaks of both signals are very closely aligned (correlated), however the red signal has additional features elsewhere which don't match the blue curve.
I am looking for some function which can tell me how correlated these two signals are at a given time. IE: at t = -18 and t = +10 where the peaks are located, the correlation should be very close to -1, while at t = -40, the correlation is probably close to 0.
Specifically, I want a robust way to tell that if I see a peak in the blue curve, then there is a corresponding (negative) peak in the red curve.
I've looked into cross correlation (https://en.wikipedia.org/wiki/Cross-correlation), however this seems suitable for time series which simply have a constant time lag with respect to each other. In my problem the correlation between my two signals is changing with time. I've thought about dividing up the signal into small bins and computing the correlation of each bin, but I was hoping there is a better way.
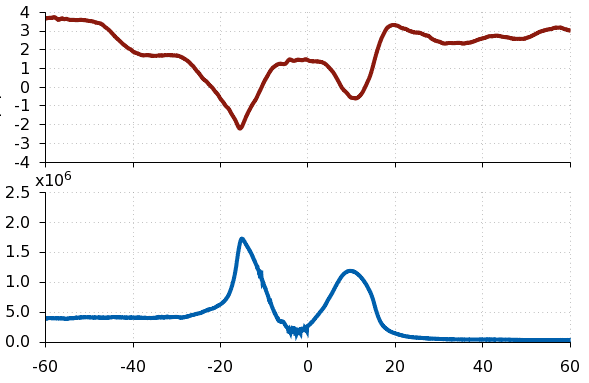
I am looking for some function which can tell me how correlated these two signals are at a given time. IE: at t = -18 and t = +10 where the peaks are located, the correlation should be very close to -1, while at t = -40, the correlation is probably close to 0.
Specifically, I want a robust way to tell that if I see a peak in the blue curve, then there is a corresponding (negative) peak in the red curve.
I've looked into cross correlation (https://en.wikipedia.org/wiki/Cross-correlation), however this seems suitable for time series which simply have a constant time lag with respect to each other. In my problem the correlation between my two signals is changing with time. I've thought about dividing up the signal into small bins and computing the correlation of each bin, but I was hoping there is a better way.