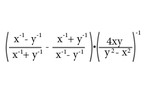How to Simplify Complex Problems: Expert Tips and Tricks

  • Context: MHB 
  • Thread starter Thread starter Canzy
  • Start date Start date
  • Tags Tags
    Simplify
Click For Summary
SUMMARY

This discussion focuses on techniques for simplifying complex mathematical fractions, specifically the expression \(\frac{\frac{1}{x} - \frac{1}{y}}{\frac{1}{x} + \frac{1}{y}}\). The initial step involves clearing complex fractions by multiplying by \(xy\), resulting in \(\frac{y - x}{y + x}\). The next strategy includes multiplying the fraction by \(\frac{y - x}{y - x}\) to transform the denominator into the difference of squares, \(y^2 - x^2\), facilitating further simplification.

PREREQUISITES
  • Understanding of basic algebraic fractions
  • Familiarity with the concept of multiplying by a conjugate
  • Knowledge of the difference of squares formula
  • Ability to manipulate algebraic expressions
NEXT STEPS
  • Study the method of simplifying complex fractions in algebra
  • Learn about the difference of squares and its applications
  • Practice multiplying fractions by their conjugates
  • Explore advanced algebraic techniques for simplifying expressions
USEFUL FOR

Students, educators, and anyone seeking to enhance their skills in algebraic simplification and problem-solving techniques.

Canzy
Messages
2
Reaction score
0
Hey guys,

I know it's pretty simple but after an hour of thinking on it i just can't get how to simplify this. Can someone help me?

Thank you in advance!
 

Attachments

  • 9.png
    9.png
    1.8 KB · Views: 90
Mathematics news on Phys.org
Canzy said:
Hey guys,

I know it's pretty simple but after an hour of thinking on it i just can't get how to simplify this. Can someone help me?

Thank you in advance!
Start by clearing the complex fractions. For example:
[math]\frac{\frac{1}{x} - \frac{1}{y}}{\frac{1}{x} + \frac{1}{y}}[/math]

[math]= \frac{\frac{1}{x} - \frac{1}{y}}{\frac{1}{x} + \frac{1}{y}} \cdot \frac{xy}{xy}[/math]

[math]= \frac{y - x}{y + x}[/math]

Now we pull a trick. Look at the fraction just above. I'm going to multiply the fraction by (y - x)/(y - x) to get the denominator to be of the form y^2 - x^2. That will cancel out the y^2 - x^2 in the last factor.

Can you finish this?

-Dan
 
Yes, i can. Thank you!
 

Similar threads

MHB How to simplify a diabolical expression involving radicals
  • · Replies 1 ·
Replies
1
Views
2K
MHB Which simplifying method should be used to simplify 2x^2y^2 times 5xy^4?
  • · Replies 1 ·
Replies
1
Views
2K
Simplify this expression for the period
  • · Replies 4 ·
Replies
4
Views
3K
MHB Negative numbers with fraction problem: simplify 3/4 [ 5/6 ( -18/25 ) + 1/2 ]
  • · Replies 9 ·
Replies
9
Views
3K
MHB Simplifying radicals - Help with basic number manipulation
  • · Replies 5 ·
Replies
5
Views
3K
Undergrad How Do I Simplify the Right Side of the Mathematical Induction Equation?
  • · Replies 9 ·
Replies
9
Views
3K
MHB Calculating Exponents for Business Model
  • · Replies 5 ·
Replies
5
Views
2K
MHB Algebraic expression simplification 2(2u+v)/u = 4(v^2-4u^2)/3u^2
  • · Replies 4 ·
Replies
4
Views
2K
Mathematica How to simplify expressions in Mathematica with log and exp in them?
  • · Replies 6 ·
Replies
6
Views
4K
Using Demorgan's Theoroem to Simplify C'+D'+A'B'CD
  • · Replies 2 ·
Replies
2
Views
1K