SUMMARY
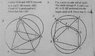
The forum discussion centers on solving complex Euclidean geometry proofs, specifically Problems 7 and 8. Users suggest redrawing figures for clarity, particularly for Problem 7, where line SB should be a diameter of circle ABC. For Problem 8, the Exterior Angle Theorem is referenced, particularly Proposition 1.32, which states that the measure of an exterior angle of a triangle equals the sum of the measures of the remote interior angles. Ultimately, one user confirms they have solved both problems and plans to share their solutions.
PREREQUISITES
- Understanding of Euclidean geometry principles
- Familiarity with the Exterior Angle Theorem
- Ability to interpret geometric figures accurately
- Knowledge of angle relationships in circles
NEXT STEPS
- Study the Exterior Angle Theorem in detail, focusing on Proposition 1.32
- Learn about the properties of angles subtended by equal arcs in circles
- Practice redrawing complex geometric figures for clarity
- Explore proofs related to quadrilaterals inscribed in circles
USEFUL FOR
Students and educators in mathematics, particularly those focusing on geometry proofs, as well as anyone looking to enhance their understanding of Euclidean geometry concepts.