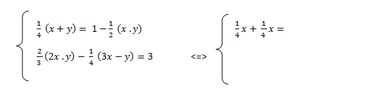SUMMARY
The discussion focuses on solving a system of simultaneous equations involving multiplication symbols represented by dots. The equations presented include $ \dfrac{x}{4} + \dfrac{x}{4} = \dfrac{x}{2} $ and $ \dfrac{x+y}{4} = 1 - \dfrac{xy}{2} $. Participants concluded that the system has no real solutions, as demonstrated through algebraic manipulation leading to a quadratic equation with no real roots. The final derived equation is $ 17x^2 + 10x + 12 = 0 $, confirming the absence of real solutions.
PREREQUISITES
- Understanding of algebraic manipulation and solving equations
- Familiarity with simultaneous equations
- Knowledge of quadratic equations and their properties
- Basic skills in handling fractions and multiplication in equations
NEXT STEPS
- Study methods for solving simultaneous equations with multiple variables
- Learn about the properties of quadratic equations and their discriminants
- Explore algebraic techniques for eliminating fractions in equations
- Investigate graphical methods for visualizing solutions to systems of equations
USEFUL FOR
Students, educators, and anyone interested in algebra, particularly those tackling simultaneous equations and quadratic equations in their studies or teaching.