Md. Abde Mannaf
- 20
- 1
Homework Statement
Homework Equations
The Attempt at a Solution
here is i am still stuck.
Don't use substitution, use Leibniz rule with α as the second variable.
Md. Abde Mannaf said:i know the Leibniz's rule. i solve many mathematical term . bt i cann't solve this math with Leibniz rule. i am still stuck
here. here limit is constant so 2nd and 3rd term will be zero.
See this, example 3.Zondrina said:if you are intending to use Leibniz rule. I for one have never seen an In\text{In} function before.
You can even cheat :) using wolframalpha.com.Md. Abde Mannaf said:Homework Statement
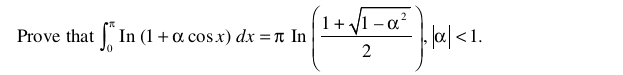
Homework Equations
The Attempt at a Solution
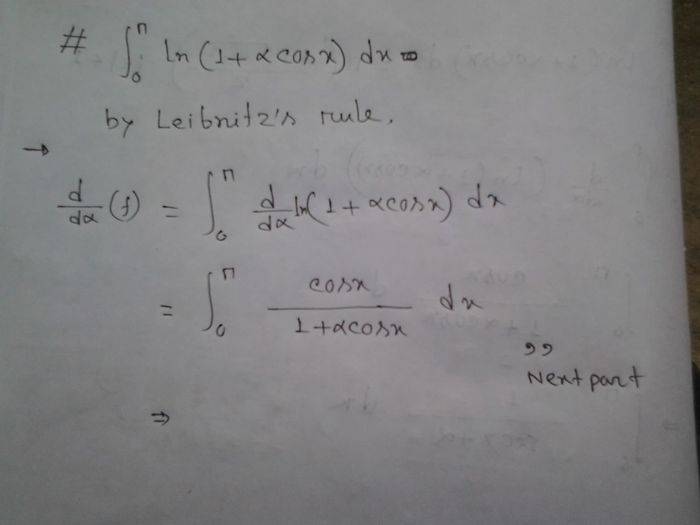
here is i am still stuck.
Zondrina said:I believe there are quite a few typos in the problem statement if you are intending to use Leibniz rule. I for one have never seen an ##\text{In}## function before.
The Leibniz rule in one dimension would be:
$$\frac{d}{dx} \int_{a(x)}^{b(x)} f(t) dt = f(b(x)) b'(x) - f(a(x)) a'(x)$$
EDIT: It would be more appropriate to call this the fundamental theorem.
Does no one read my posts :-)ehild said:You can even cheat :) using wolframalpha.com.
You can write your integral for ##f'(\alpha)## as ##\int_0^{\pi/2} + \int_{\pi/2}^{\pi}##, then change variables to ##x \leftarrow \pi -x## in the second integral, to getMd. Abde Mannaf said:i could not solve this math above analysis . i am trying to my best. but i am fail every time. and again try...
please see this and give me more idea to solve
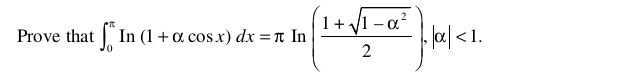
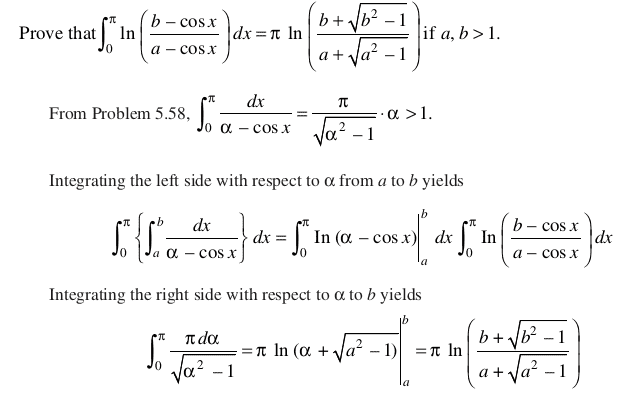
##\int \frac{1}{1+\alpha cos(x)} dx## is not that nasty.certainly said:Now let's do that daunting looking integral. Like I said before, this is a good problem.
First write ##\int_0^{\pi} \frac{1}{\alpha}-\frac{1}{(\alpha)(1+\alpha cos(x))} dx## for the original integral.
However ##\int \frac{1}{1+\alpha cos(x)} dx## itself is not nice, in-fact it's pretty nasty.
Yeah, your right. I didn't actually do the integral, I only saw the answer and thought, this might take some time.ehild said:##\int \frac{1}{1+\alpha cos(x)} dx## is not that nasty.
Use the identity ##\cos(x)=\frac{1-\tan^2(x/2)}{1+\tan^2(x/2)}##. Substitute u=tan(x/2), x=2arctan(u), ##dx=\frac{2}{1+u^2}du##. The integration limits become 0-->infinite.