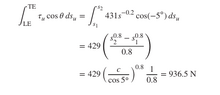SUMMARY
The discussion centers on a mathematical problem from "Fundamentals of Aerodynamics" by Anderson, specifically example 1.1 on page 26. Participants analyze the integration of the term ##s^{-0.2}## into ##\dfrac{s^{0.8}}{0.8}## using the antiderivative rule for exponents. The confusion arises regarding the relationship between the variables c, s, and the integration process, particularly how ##\dfrac{c}{\cos 5°}## relates to the lengths of vectors in the problem. The conclusion suggests that setting s1 to zero simplifies the equation, allowing for the cancellation necessary to equate the terms.
PREREQUISITES
- Understanding of basic calculus, specifically integration and antiderivative rules.
- Familiarity with the Mean Value Theorem of integration.
- Knowledge of trigonometric functions and their applications in geometry.
- Ability to interpret mathematical notation and expressions in physics contexts.
NEXT STEPS
- Study the antiderivative rule for exponents in calculus.
- Explore the Mean Value Theorem of integration and its applications.
- Review trigonometric identities and their geometric interpretations.
- Practice problems from "Fundamentals of Aerodynamics" to reinforce understanding of the concepts discussed.
USEFUL FOR
Students of aerodynamics, physics enthusiasts, and anyone studying calculus who seeks to deepen their understanding of integration and its applications in real-world problems.
 equal to
equal to
 ? How was the 0.8 exponent taken out of the equation to make space for c/cos5?
? How was the 0.8 exponent taken out of the equation to make space for c/cos5?