sgfw
- 15
- 0
y = 2.5*(fresnelC(t*2) - arcsinh(t/2))
x = 2.5*(fresnelS(t) + arcsinh(t/2))
In case you don't have anything that can graph this, this is what it looks like from t = -2*pi to 2*pi, from y = -7 to 7, and from x= -7 to 7:
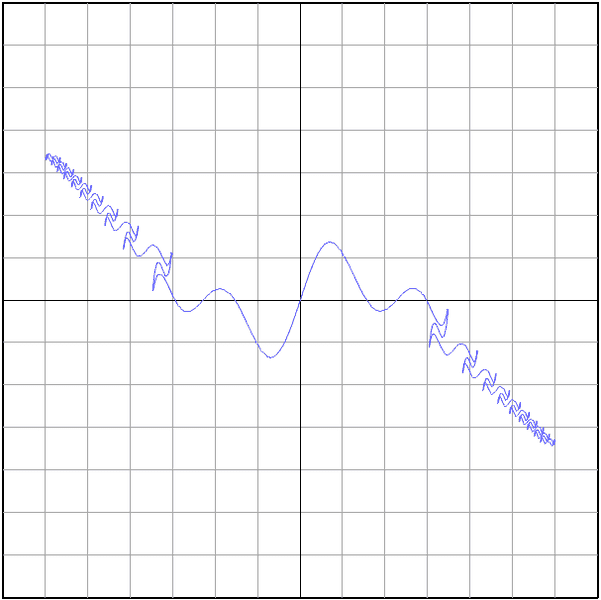
There are a lot of interesting ones that can be made with the fresnel integrals, but I won't list the other ones that I found because they are all pretty similar.
Do you have any cool equations? I tried looking online, but the ones I could find weren't all that great.
x = 2.5*(fresnelS(t) + arcsinh(t/2))
In case you don't have anything that can graph this, this is what it looks like from t = -2*pi to 2*pi, from y = -7 to 7, and from x= -7 to 7:
There are a lot of interesting ones that can be made with the fresnel integrals, but I won't list the other ones that I found because they are all pretty similar.
Do you have any cool equations? I tried looking online, but the ones I could find weren't all that great.
Last edited: