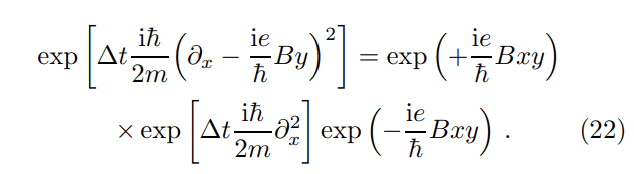SUMMARY
The discussion centers on deriving equation (22) from the paper linked by the user, which involves the identity of operators in quantum mechanics. The key formula presented is $$(\partial_x - \mathrm{i} e/\hbar By)\psi (\vec{x}) = \exp(\mathrm{i} e B x y/\hbar) \partial_x \left [\exp(-\mathrm{i} e B x y/\hbar) \psi(\vec{x}) \right].$$ This identity is established through the iterative application of the operator, demonstrating that for any natural number k, $$(\partial_x - \mathrm{i} e/\hbar By)^k\psi (\vec{x})$$ can be expressed in terms of the exponential operator. The conclusion confirms that the commutation relation ##[\partial _x, y] = 0## plays a crucial role in this derivation.
PREREQUISITES
- Understanding of quantum mechanics operators
- Familiarity with the Baker-Campbell-Hausdorff (BCH) formula
- Knowledge of operator exponentiation in quantum mechanics
- Proficiency in LaTeX for mathematical expressions
NEXT STEPS
- Study the Baker-Campbell-Hausdorff formula in detail
- Explore operator exponentiation techniques in quantum mechanics
- Review commutation relations and their implications in quantum systems
- Analyze additional examples of operator identities in quantum mechanics literature
USEFUL FOR
Physicists, mathematicians, and students specializing in quantum mechanics, particularly those interested in operator theory and mathematical derivations in quantum field theory.