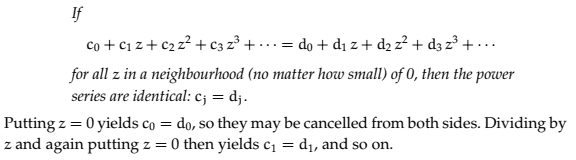SUMMARY
The discussion centers on the validity of a proof related to the Identity Theorem for power series. Participants highlight that the proof's assumption of dividing by ##z##, while excluding ##z=0##, leads to a flawed argument. They emphasize that the theorem holds true even if two series are equal only on an infinite sequence of points converging to ##0##. Furthermore, continuity at ##0## must be established, typically proven by demonstrating uniform convergence of power series on compact subsets within their radius of convergence.
PREREQUISITES
- Understanding of power series and their convergence properties.
- Familiarity with the Identity Theorem in complex analysis.
- Knowledge of limits and ε-δ definitions in calculus.
- Concept of uniform convergence and its implications for continuity.
NEXT STEPS
- Study the Identity Theorem for power series in complex analysis.
- Learn about uniform convergence and its role in the continuity of functions defined by power series.
- Explore the implications of limits in the context of power series and their coefficients.
- Investigate the conditions under which power series converge uniformly on compact subsets.
USEFUL FOR
Mathematicians, students of complex analysis, and anyone interested in the properties and proofs related to power series and their convergence behavior.