SUMMARY
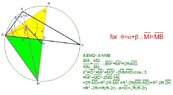
The discussion focuses on proving the relationship between the distance \(d\) between the circumcenter \(O\) and incenter \(I\) of triangle \(ABC\) and the radii \(R\) and \(r\) of the circumcircle and incircle, respectively. The established formula is \(d = \sqrt{R(R - 2r)}\). Participants provided geometric insights and algebraic manipulations to derive this formula, emphasizing its significance in triangle geometry.
PREREQUISITES
- Understanding of triangle geometry, specifically circumcenters and incenters.
- Familiarity with the properties of incircles and circumcircles.
- Knowledge of the relationship between triangle sides, angles, and their respective radii.
- Basic algebraic manipulation skills for geometric proofs.
NEXT STEPS
- Study the derivation of the circumradius \(R\) and inradius \(r\) formulas for various triangle types.
- Explore the implications of the formula \(d = \sqrt{R(R - 2r)}\) in advanced triangle geometry.
- Investigate the relationship between triangle area and its inradius and circumradius.
- Learn about the Euler line and its connection to the circumcenter and incenter.
USEFUL FOR
Mathematicians, geometry enthusiasts, and students studying advanced triangle properties will benefit from this discussion, particularly those interested in geometric proofs and relationships between triangle centers.