- #1
Marko7
- 8
- 0
I want to calculate eccentric anomaly of all points of ellipse-circle intersection.
Ellipse is not rotated and its center is in origin.
Circle can be translated to (Cx, Cy) coordinates.
I am using python for calculations.
Only solution I found, is this:
https://math.stackexchange.com/questions/3419984/find-the-intersection-of-a-circle-and-an-ellipse
And I implemented it in my code. I avoided calculating polynomial roots manually by using numpy's solver.
I tested it on some simple example:
>>> ellipse_circle(5, 2.17945, 4.5, 0, 1)
array([5.22599703, 1.05718828])
But those two roots are not eccentric anomalies of intersection points, as can be seen here (Point D is real intersection, and point A is calculated one):
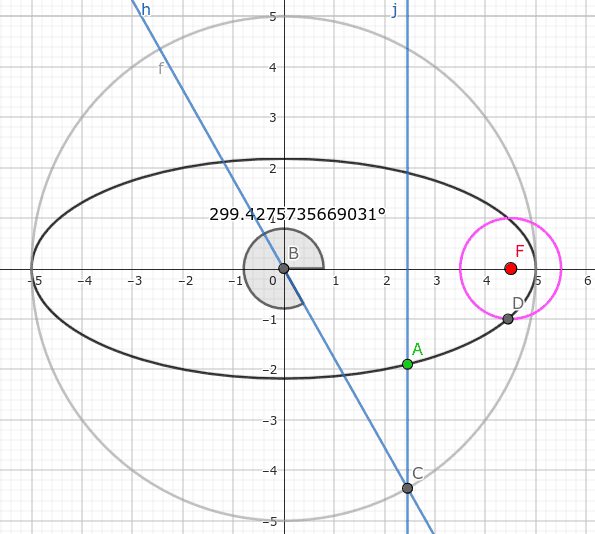
So, what am I doing wrong, how can I calculate eccentric anomaly?
Ellipse is not rotated and its center is in origin.
Circle can be translated to (Cx, Cy) coordinates.
I am using python for calculations.
Only solution I found, is this:
https://math.stackexchange.com/questions/3419984/find-the-intersection-of-a-circle-and-an-ellipse
And I implemented it in my code. I avoided calculating polynomial roots manually by using numpy's solver.
ellipse_circle.py:
import numpy as np
def ellipse_circle(a, b, c_x, c_y, r):
"""Calculate eccentric anomalies of intersecting points
on non-rotated ellipse in origin, and translated circle"""
# quartic equation coefficients
a_4 = a**2 * (c_y**2 - b**2) + b**2 * (c_x - r)**2
a_3 = 4 * a**2 * r * c_y
a_2 = 2 * (a**2 * (c_y**2 - b**2 + 2*r**2) + b**2 * (c_x**2 - r**2))
a_1 = 4 * a**2 * r * c_y
a_0 = a**2 * (c_y**2 - b**2) + b**2 * (c_x + r)**2
# quartic equation roots
roots = np.polynomial.polynomial.polyroots([a_0, a_1, a_2, a_3, a_4])
# take only non-complex roots
real_roots = np.real(roots[np.isreal(roots)])
return real_roots % (2*np.pi)I tested it on some simple example:
>>> ellipse_circle(5, 2.17945, 4.5, 0, 1)
array([5.22599703, 1.05718828])
But those two roots are not eccentric anomalies of intersection points, as can be seen here (Point D is real intersection, and point A is calculated one):
So, what am I doing wrong, how can I calculate eccentric anomaly?