Individual Spherical Capacitors

In summary: Look at the attachment. In summary, two conducting spheres of radii R1 and R2 have individual capacitances of 4\pi\epsilon_oR_1 and 4\pi\epsilon_oR_2 respectively. When connected by a metal wire, the combination acts as parallel capacitors, with a resulting capacitance of (Q1+Q2)/V. If the spheres are connected to a battery, they are still in parallel but the battery will short circuit.
  • #1
Saitama
4,243
93

Homework Statement


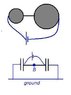
Two conducting spheres of radii R1 and R2 are kept widely separated from each other. What are their individual capacitance? If the spheres are connected by a metal wire, what will be the capacitance of the combination? Think in terms of series-parallel connections.


Homework Equations





The Attempt at a Solution


Individual capacitance are simply [itex]4\pi\epsilon_oR_1[/itex] and [itex]4\pi\epsilon_oR_2[/itex]. I have no idea on what happens when they are connected. I can't understand the type of combination. Will it be series or parallel?

Any help is appreciated.
 
Physics news on Phys.org
  • #2
A single spherical shell is a capacitor only if you imagine that the other shell (ground) is at infinitity. Now, when you connect the two spheres together, you join a set of plates of each of the capacitors together, and hold them at a fixed potential? What happens to the "other plates"? Is this connection in series or parallel?
 
  • #3
Sorry but i have no idea, can you provide me some more explanation?
 
  • #4
What does it mean for capacitors to be connected in series? How about in parallel?
 
  • #5
Remember the definition of capacitance: C=Q/V. V is the potential with respect to infinity in this case. The shape does not count, any kind of a metal piece has capacitance.
Charge the spheres to equal potential. Q1=C1V, Q2=C2V. Connect them with a wire. What happens? What is the potential of this structure? What is the net charge on it? So what is the capacitance?

ehild
 
  • #6
Dickfore said:
What does it mean for capacitors to be connected in series? How about in parallel?

If the capacitors are in series, the charge is same and if they are in parallel, the potential is same.

ehild said:
Remember the definition of capacitance: C=Q/V. V is the potential with respect to infinity in this case. The shape does not count, any kind of a metal piece has capacitance.
Charge the spheres to equal potential. Q1=C1V, Q2=C2V. Connect them with a wire. What happens? What is the potential of this structure? What is the net charge on it? So what is the capacitance?

ehild

Nothing should happen as they are at same potential.
 
  • #7
And what is the charge of the whole system?

ehild
 
  • #8
ehild said:
And what is the charge of the whole system?

ehild

The charge is (C1+C2)V.
And capacitance is (C1+C2).
 
  • #9
Splendid! So it is like parallel capacitors.

ehild
 
  • #10
ehild said:
Splendid! So it is like parallel capacitors.

ehild

Yes, but in the question its not mentioned that they are at same potential.
 
  • #11
Well, if they are connected with a wire, they become the same potential anyway.

The capacitance does not depend on the charge or on the potential. But you can determine it by measuring charge and potential, and taking the ratio C=Q/V.

It is the same as with the mass. m=F/a, mass equals to force over acceleration. The mass of the object is its attribute, but you can measure it by applying a known force and detecting the acceleration.

If you know the charge of an object and its potential with respect to infinity you can attribute a capacitance to it as C=Q/V.

If your spheres are at different potential initially, after connecting them, there will be some charge transfer from one sphere to the other, till both of them have he same potential V=kQ1/R1=kQ2/R2. The first sphere is charged to Q1=VR1/k, the second one is charged to Q2=VR2/k. The resultant capacitance is (Q1+Q2)/V.

ehild
 
  • #12
ehild said:
Well, if they are connected with a wire, they become the same potential anyway.

The capacitance does not depend on the charge or on the potential. But you can determine it by measuring charge and potential, and taking the ratio C=Q/V.

It is the same as with the mass. m=F/a, mass equals to force over acceleration. The mass of the object is its attribute, but you can measure it by applying a known force and detecting the acceleration.

If you know the charge of an object and its potential with respect to infinity you can attribute a capacitance to it as C=Q/V.

If your spheres are at different potential initially, after connecting them, there will be some charge transfer from one sphere to the other, till both of them have he same potential V=kQ1/R1=kQ2/R2. The first sphere is charged to Q1=VR1/k, the second one is charged to Q2=VR2/k. The resultant capacitance is (Q1+Q2)/V.

ehild

Thank you very much for your explanation! :smile:

This is just a question out of curiosity.
What if i connected the whole system with the battery? Will they be in series or parallel?
 
  • #13
Pranav-Arora said:
What if i connected the whole system with the battery? Will they be in series or parallel?

What do you mean? Connect one of the spheres with one lead, and the other sphere with the other lead of the battery?
 
  • #14
Dickfore said:
What do you mean? Connect one of the spheres with one lead, and the other sphere with the other lead of the battery?

Oh yes, that's what i mean. :)
 
  • #15
Pranav-Arora said:
Oh yes, that's what i mean. :)

I told you. Each spherical capacitor has the other of its plates at infinity (and all these plates may be thought of as connected to the ground). If you draw the relevant diagram, you will immediately conclude if they are connected in series or parallel.
 
  • #16
See attachment. The connected spheres as capacitors are analogous to two "normal" grounded capacitor with the free plates connected. They are in parallel between B and the ground. What happens if you connect a battery in the way you said: one terminal to one plate of the first capacitor and the other terminal to the connected plate of the other capacitor?

See the connected spheres. They are of metal. So you make a metallic contact between the terminals of the battery. It is called "short", fatal for a battery. It gets very hot and starts to smoke and gets black and it is not a battery any more... RIP...

In case of a sphere as capacitor the other "plate" is at infinity. You need to connect the terminals of the battery to the wire connecting the spheres and to the other common point of the capacitors, which is at infinity.

ehild
 

Attachments

  • spherecap.JPG
    spherecap.JPG
    10.1 KB · Views: 539
  • #17
ehild said:
See attachment. The connected spheres as capacitors are analogous to two "normal" grounded capacitor with the free plates connected. They are in parallel between B and the ground. What happens if you connect a battery in the way you said: one terminal to one plate of the first capacitor and the other terminal to the connected plate of the other capacitor?

See the connected spheres. They are of metal. So you make a metallic contact between the terminals of the battery. It is called "short", fatal for a battery. It gets very hot and starts to smoke and gets black and it is not a battery any more... RIP...

In case of a sphere as capacitor the other "plate" is at infinity. You need to connect the terminals of the battery to the wire connecting the spheres and to the other common point of the capacitors, which is at infinity.

ehild

Thank you ehild for the explanation, it was an interesting read. :smile:
 

1. What is an individual spherical capacitor?

An individual spherical capacitor is a type of capacitor that consists of two concentric spherical conductors, separated by a dielectric material. It is used to store electrical energy by creating an electric field between the two conductors.

2. How does an individual spherical capacitor work?

An individual spherical capacitor works by storing electrical energy in the form of an electric field. When a voltage is applied to the capacitor, one conductor becomes positively charged while the other becomes negatively charged. The dielectric material between them prevents the charges from coming into direct contact, thus storing the energy in the form of an electric field.

3. What are the main components of an individual spherical capacitor?

The main components of an individual spherical capacitor are the two conductors, typically made of metal, and the dielectric material, which can be a variety of materials such as air, paper, or plastic. The conductors are connected to terminals to allow for the flow of current.

4. What factors affect the capacitance of an individual spherical capacitor?

The capacitance of an individual spherical capacitor is affected by several factors including the size and distance between the two conductors, the type of dielectric material used, and the voltage applied. Generally, the larger the conductors and the closer they are together, the higher the capacitance will be.

5. What are some common applications of individual spherical capacitors?

Individual spherical capacitors have various applications, including energy storage in electronic devices, power factor correction in electrical systems, and as filters in electronic circuits. They are also commonly used in high-voltage power supplies and in radio frequency applications.

Similar threads

Why Capacitors in Parallels vs. Series: Coaxial Capacitor Case
    • Introductory Physics Homework Help
Replies
2
Views
831
Equivalent capacitance of a system of 2 spheres
    • Introductory Physics Homework Help
Replies
3
Views
3K
Why Do Capacitors Behave Differently in Series and Parallel Configurations?
    • Introductory Physics Homework Help
Replies
20
Views
402
Why can we model spherical capacitor with two dielectrics as two capacitors in series?
    • Introductory Physics Homework Help
Replies
4
Views
357
Charge on a grounded conducting sphere in a uniform electric field, after ungrounding and movement
    • Introductory Physics Homework Help
Replies
1
Views
142
Find Radius of Outer Sphere for 1uF Spherical Condenser
    • Introductory Physics Homework Help
Replies
4
Views
961
Find the capacitance of a half-full capacitor
    • Introductory Physics Homework Help
Replies
12
Views
2K
Find the unknown capacity of two capacitors
    • Introductory Physics Homework Help
Replies
5
Views
896
Equivalent capacitance of capacitors
    • Introductory Physics Homework Help
Replies
4
Views
4K
How to find the charge on each capacitor
    • Introductory Physics Homework Help
Replies
3
Views
2K

Hot Threads

Recent Insights

Back
Top