Induction: Each square can be covered by L-stones

In summary, the conversation discusses a problem involving a square with the side length $2^n$ being divided into sub-squares and one of the sub-squares being removed. The goal is to cover the remaining sub-squares without overlapping using L-stones. The conversation then moves on to discussing the possibility of using a drawing of the case $n=2$ to solve the case $n=3$ through induction.
  • #1
mathmari
Gold Member
MHB
5,049
7
Hey! :eek:

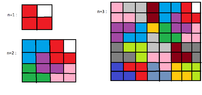
A square with the side length $2^n$ length units (LU) is divided in sub-squares with the side length $1$. One of the sub-squares in the corners has been removed. All other sub-squares should now be covered completely and without overlapping with L-stones. An L-stone consists of three sub-squares that together form an L.

I want to draw the problem for the first three cases described above ($1 \leq n \leq 3$). Then I want to show the following using induction:

For all $n \in N$ the square with side length $2^n$ LU can be covered completely and without overlapping with L-stones, after one of the sub-squares in the corners has been removed.
For the first part:

View attachment 9354

Is the drawing correct? (Wondering)
 

Attachments

  • L_stones.png
    L_stones.png
    2.6 KB · Views: 74
Last edited by a moderator:
Physics news on Phys.org
  • #2
Can we use the sketch of the case $n=2$ to get the one of the case $n=3$ ? (Wondering)

Is it maybe as follows?

The upper right sub-square is the one of case $n=2$. For the other sub-squares we have to fill them completely.

(Wondering)
 
  • #3
mathmari said:
Can we use the sketch of the case $n=2$ to get the one of the case $n=3$ ? (Wondering)

Is it maybe as follows?

The upper right sub-square is the one of case $n=2$. For the other sub-squares we have to fill them completely.

Hey mathmari!

I think so yes.
Suppose we use the same case $n=2$ square to fill each of the 4 sub squares of the case $n=3$.
Then we have 3 cells left that we still have to fill don't we?
Can we align them so that we can put another L-square into it? (Wondering)
 
  • #4
Klaas van Aarsen said:
I think so yes.
Suppose we use the same case $n=2$ square to fill each of the 4 sub squares of the case $n=3$.
Then we have 3 cells left that we still have to fill don't we?
Can we align them so that we can put another L-square into it? (Wondering)

To do that we have to make the empty cell in that corner so that the three empty cells make a L, or not? (Wondering)
 
  • #5
mathmari said:
To do that we have to make the empty cell in that corner so that the three empty cells make a L, or not?

Yes. So the sub squares at left-top, left-bottom, and right-bottom would have their empty cell at the center.
Those empty cells have the shape of an L then, allowing for another piece. (Thinking)
 
  • #6
Klaas van Aarsen said:
Yes. So the sub squares at left-top, left-bottom, and right-bottom would have their empty cell at the center.
Those empty cells have the shape of an L then, allowing for another piece. (Thinking)

I see! Thanks a lot! (Mmm)
 

FAQ: Induction: Each square can be covered by L-stones

What is induction and how does it relate to covering squares with L-stones?

Induction is a mathematical proof technique used to prove statements about infinite sets. In this case, we are using induction to prove that each square on a chessboard can be covered by L-shaped stones. This means that no matter how large the chessboard is, we can always find a way to cover all the squares using L-stones.

How does the induction process work in this scenario?

In this scenario, we start by proving that the statement is true for the smallest possible case, which is a 1x1 chessboard. Then, we assume that the statement is true for a general case, such as an nxn chessboard. Finally, we use this assumption to prove that the statement is also true for the next case, which would be an (n+1)x(n+1) chessboard. This process continues until we have proven that the statement is true for all possible cases.

Can you provide an example of how the induction process would work for covering a 4x4 chessboard?

Sure! First, we prove that a 1x1 chessboard can be covered by 1 L-stone. Then, we assume that a 4x4 chessboard can be covered by L-stones. Using this assumption, we can show that a 5x5 chessboard can also be covered by L-stones. Since we have proven that the statement is true for the previous case (4x4), we can conclude that it is also true for a 5x5 chessboard. This process can be repeated to prove that the statement is true for any size chessboard.

Are there any limitations to using induction to prove this statement?

Induction can only be used to prove statements about infinite sets, so it may not be applicable in all scenarios. Additionally, the statement must be true for the base case (1x1 chessboard) and the general case (nxn chessboard) in order for the proof to be valid.

Can the induction process be used to prove that each square can be covered by other shapes besides L-stones?

Yes, the induction process can be used to prove that each square can be covered by other shapes as long as the statement is true for the base case and the general case. However, the process may vary depending on the specific shape being used.

Similar threads

MHB Can L-Shaped Tiles Fit Perfectly on a 2xn Board If n Is Not Divisible by 3?
Replies
4
Views
2K
I Mutual inductance in a transformer
Replies
16
Views
2K
I Can you use proof by contradiction in the midst of induction
Replies
3
Views
2K
Cantor set ℵ , inductive proofs by openly counting.
Replies
11
Views
3K
MHB Is the Intersection of Intervals Empty?
Replies
8
Views
2K
Inductance of Square Coil Antenna on PCB
Replies
7
Views
3K
Probability of Outcomes in Merge Shuffle
Replies
1
Views
2K
System of two pulleys and three masses
Replies
22
Views
4K
Max Temp of Water Around Heated Square Rod
Replies
2
Views
1K
MHB Induction to find the determinant
Replies
2
Views
3K

Hot Threads

Recent Insights

Back
Top