CB4
- 10
- 0
I'm currently taking a Semiconductor class and we're talking about Schrödinger's Wave Equation, specifically the 1 dimensional time independent form.
We were looking at the infinite potential well model:
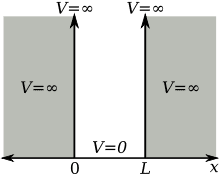
And we divided the graph into 3 different regions: first being the left (or negative) V(x)= -inf, the second being V(x)=0, and the third being V(x)= inf.
We solved the second region first using the equation:
d2\Psi(x)/dx2 + \frac{2m}{\hbar}*(E-V(x))*\Psi(x) = 0
Well my professor said this math should be something we could do easily, so pardon me if I seem a bit ignorant, but I really can't recall an effective way to tackle this problem. He gave us the solution, which is:
\Psi(x) = A1cos(kx) + A2sin(kx)
I should have included all the information needed, but if not please ask!
Thanks!
We were looking at the infinite potential well model:
And we divided the graph into 3 different regions: first being the left (or negative) V(x)= -inf, the second being V(x)=0, and the third being V(x)= inf.
We solved the second region first using the equation:
d2\Psi(x)/dx2 + \frac{2m}{\hbar}*(E-V(x))*\Psi(x) = 0
Well my professor said this math should be something we could do easily, so pardon me if I seem a bit ignorant, but I really can't recall an effective way to tackle this problem. He gave us the solution, which is:
\Psi(x) = A1cos(kx) + A2sin(kx)
I should have included all the information needed, but if not please ask!
Thanks!