Instantaneous Center of Velocity

[medwatt]

Hello,
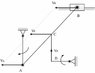
I am trying to find the angular velocity of a link in a 4 link mechanism problem but I have reached a scenario which is new to me. Please look at the attached image.
I already know the velocity of the slider which is 3m/s. I have indicated in the diagram a line parallel to AB to indicate that all points on AB have the same velocity, hence AB undergoes only translation.
My problem is finding the velocity at point D because when I try to draw the instantaneous Center of velocity of points C and D they two velocities are concurrent. I seem to have a lot of ways to interpret it which is the problem. One way I can look at it is to say that C is the ICV which is absurd since I have already established that C, being on AB which is a rigid rod already has a velocity of 3.
Please enlighten me !

 

[256bits]

I am not sure what you mean by C and D have velocities which are concurrent. It might have been better to use a more explicit term.

Are you sure AB undergoes only translation. It seems that point A would have some rotation since the rod connecting A to its base can only rotate. So one can say the velocity vectors Vb <> Vc <> Va.
Same with point D having only rotation being connected to its base.
Point C will be a function of translation and rotation.

Only at the instant shown, are the magnitudes of Vb=Vc=Va, and Vd=0. At all other times the magnitudes are completely different, as are the directions of velocity.

 

[medwatt]

I meant they are concurrent at the instance shown in the diagram. AB undergoes plane motion but at the instance shown since Va=Vb it appears momentarily that AB is translating.
I am still unsure what is Vd and the angular speed of link CD at the instance shown ??
If we say Vd=0 then by Vd=wR, it implies that w=0 which can't be because the crank is turning.

 

[256bits]

You do not want to set up your equations from just this one instance depicted in the picture, but for the a range of motion as the slider moves along. One instance after as B has moved along the slider the whole of the angles and velocities of the points have changed. Your job is to find an equation that can determine the velocities of A, C, or D at any other time.

You already know several items
Vb is pure translation
Va and Vc both have translation ( since they are on the same arm as Vb ) but also a superimposed rotation since they each are connected to another arm that is rotating. Vc in its case is connected to 2 arms, one of which can only rotate.

You also know that Va has a velocity about OA equal to wr ( w is angular velocity of arm OA and r is the length of arm OA ). You also know that this velocity must be the same as when calculating the velocity of A with reference to its translation and rotation about point B. I hope I said that correctly.
Vao = Vab + Vb
Or velocity of A relative to O equals velocity of A relative to B + the velocity of B.

And you continue the same line of reasoning with the other linkages.

perhaps if you read this
http://www.roymech.co.uk/Useful_Tables/Mechanics/Linkages.html
you will gain some idea of how to tackle the problem.
Your kinematics textbook should have some exampes also.

I haven't done these types of relative velocity problems for some while, and do not want to give an incorrect velocity of one point relative to another that may be incorrect.

In the meantime I will try to look up a site with a better explanation if there is one around on the WWW