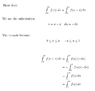SUMMARY
The discussion focuses on understanding the computation of new bounds during the process of u-substitution in integral calculus, specifically when substituting from variable x to variable u. Participants clarify that the bounds of integration change based on the substitution, with the example of u = x - a illustrating how to derive new bounds from the original inequality 0 ≤ x ≤ a. The conversation emphasizes that both u and x are dummy variables in integration, allowing for interchangeability in expressions like f(u) and f(x) once the integrand is in the same form.
PREREQUISITES
- Understanding of integral calculus and u-substitution
- Familiarity with inequalities and their manipulation
- Knowledge of dummy variables in integration
- Basic algebraic skills for substitution
NEXT STEPS
- Study the process of u-substitution in integral calculus
- Learn about the properties of dummy variables in mathematical expressions
- Explore examples of changing bounds in definite integrals
- Review inequalities and their applications in calculus
USEFUL FOR
Students of calculus, mathematics educators, and anyone seeking to deepen their understanding of integral bounds and variable substitution techniques.