Ali Durrani
- 55
- 5
Hello guys!
can i get the derivation for this equation ?
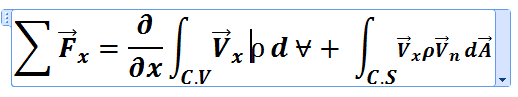
can i get the derivation for this equation ?
The integral form of the momentum equation is critical in fluid dynamics, specifically regarding the conservation of x-momentum within a control volume. The first term in the equation represents the time rate of accumulation of x-momentum, denoted by a partial derivative with respect to time (t). The second term indicates the net rate of x-momentum exiting the control volume. Understanding these components is essential for correctly applying the momentum equation in fluid mechanics.
PREREQUISITESStudents and professionals in fluid mechanics, engineers working on fluid dynamics problems, and educators teaching conservation laws in physics will benefit from this discussion.
yes sir as you said the 1st term should be the partial derivative with respect to time but i don't know why our teacher in the fluid class wrote the equation in this form, and it was not a mistake because he used it again and again, can you explain the logic behind it as he is a very senior teacher and he wouldn't make such a silly mistakeChestermiller said:I think the first term should be a partial derivative with respect to time t (not x), and represents the rate of accumulation of x-momentum within the control volume. The second term represents the net rate of x-momentum leaving the control volume.
I stand by what I said. I can't account for what your teacher does. All I can do is confidence in what I am saying.Ali Durrani said:yes sir as you said the 1st term should be the partial derivative with respect to time but i don't know why our teacher in the fluid class wrote the equation in this form, and it was not a mistake because he used it again and again, can you explain the logic behind it as he is a very senior teacher and he wouldn't make such a silly mistake
No problem.Ali Durrani said:sorry i asked him and he said its partial by partial t and not x his writing style is different so i mistakenly wrote it as partial by partial x