- #1
Ali Durrani
- 56
- 5
Hello guys!
can i get the derivation for this equation ?
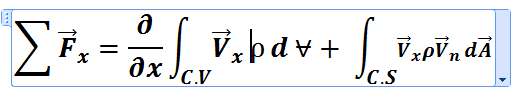
can i get the derivation for this equation ?
yes sir as you said the 1st term should be the partial derivative with respect to time but i don't know why our teacher in the fluid class wrote the equation in this form, and it was not a mistake because he used it again and again, can you explain the logic behind it as he is a very senior teacher and he wouldn't make such a silly mistakeChestermiller said:I think the first term should be a partial derivative with respect to time t (not x), and represents the rate of accumulation of x-momentum within the control volume. The second term represents the net rate of x-momentum leaving the control volume.
I stand by what I said. I can't account for what your teacher does. All I can do is confidence in what I am saying.Ali Durrani said:yes sir as you said the 1st term should be the partial derivative with respect to time but i don't know why our teacher in the fluid class wrote the equation in this form, and it was not a mistake because he used it again and again, can you explain the logic behind it as he is a very senior teacher and he wouldn't make such a silly mistake
No problem.Ali Durrani said:sorry i asked him and he said its partial by partial t and not x his writing style is different so i mistakenly wrote it as partial by partial x
The integral form of the momentum equation is a mathematical representation of the conservation of momentum in a fluid system. It takes into account the change in momentum within a control volume over time.
The differential form of the momentum equation is based on the local properties of a fluid, while the integral form considers the overall behavior of a fluid within a control volume. The integral form is derived by integrating the differential form over the control volume.
The integral form of the momentum equation includes terms for the convective flux, pressure forces, body forces, and viscous forces. These terms represent the different mechanisms by which momentum can be transferred in a fluid system.
The integral form of the momentum equation is used in various engineering and scientific fields, such as fluid mechanics and aerodynamics, to analyze and predict the behavior of fluids in different scenarios. It can be solved numerically using computational fluid dynamics methods to obtain valuable insights and make predictions about fluid flow.
The integral form of the momentum equation assumes that the fluid is incompressible, the control volume is stationary, and there are no external forces acting on the control volume. It also assumes that the fluid properties are constant within the control volume and there are no sharp variations in the flow field.