Prometheus18
- 3
- 1
Hello all. I'm using Griffiths' Introduction to Quantum Mechanics (3rd ed., 2018), and have come across what, on the face of it, seems a fairly straightforward principle, but which I cannot justify to myself. It is used, tacitly, in the first equation in the following worked example:

The putative justification is in the fact that the |x> eigenstates form a complete basis and the following identity, which I conpletely understand, holds:
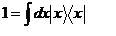
My problem is this: How does one justify moving the integral sign and dx outside of the outer brackets here? There is integration over the right hand part, and even the state vector S(t), given that it's not a function of x, can be rightly brought inside the integral but how do we justify moving the <p|x part inside it, if there's no summation over that part (and x hat and p both obviously depend on x)?
To be honest, I also fail to understand the second legerdemain, mentioned this time by Mr Griffiths (below the first equation); it's true that x is, in a certain sense, an eigenvalue of |x>, of course, but only if we accept a continuous spectrum of eigenvalues; it fails to be an eigenvalue at all if it's a constant, which appears to negate what Mr Griffiths is saying, unless I'm mistaken.
I know most students would probably gloss over these sorts of issues on a worked example without a second thought but the way I see it is that that will cause issues further down the line on actual assignments.
The putative justification is in the fact that the |x> eigenstates form a complete basis and the following identity, which I conpletely understand, holds:
My problem is this: How does one justify moving the integral sign and dx outside of the outer brackets here? There is integration over the right hand part, and even the state vector S(t), given that it's not a function of x, can be rightly brought inside the integral but how do we justify moving the <p|x part inside it, if there's no summation over that part (and x hat and p both obviously depend on x)?
To be honest, I also fail to understand the second legerdemain, mentioned this time by Mr Griffiths (below the first equation); it's true that x is, in a certain sense, an eigenvalue of |x>, of course, but only if we accept a continuous spectrum of eigenvalues; it fails to be an eigenvalue at all if it's a constant, which appears to negate what Mr Griffiths is saying, unless I'm mistaken.
I know most students would probably gloss over these sorts of issues on a worked example without a second thought but the way I see it is that that will cause issues further down the line on actual assignments.
