MidgetDwarf
- 1,608
- 716
- Homework Statement
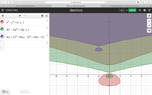
- Let $$ A = { (x,y) : x^2 -y^3 +4y \leq 1}$$ . Now let B be the set obtained asymmetrically scaling A by a factor of 3 in the x-direction, and by a factor of 4 in the y-direction, then translating the scale set by the vector <-2,5>. Use a graphing tool to show A and B.
- Relevant Equations
- $$ h(x,y) = x^2 -y^3 +4y \leq 1$$
What does asymmetrically scaling mean?
I am unsure of how to do this problem. I am thinking $$ h(3x,4y) = 9x^2 \ - \ 64y^3 \ + \ 16y \leq 1$$, which gives us the scaling we want in the x-direction and y-direction.
Now, for the translation of points of A by the vector <-2, 5>. I am unsure.
I am a bit embarrassed posting this. It appears that this problem is just a linear transformation problem.
This problem is for fun, and not a hw exercise.
I have attached a graph of the set A.
Here we go!