Interesting theorem, complex eigenvalues.

[bobby2k]

Take a look at this theorem.

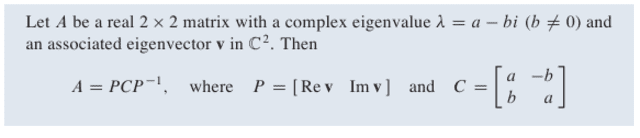
Is it a way to show this theorem? I would like to show it using the standard way of diagonalizing a matrix.

I mean if P = [v1 v2] and D =
[lambda1 0
0 lambda D]

We have that AP = PD even for complex eigenvectors and eigenvalues.

But the P matrix in this theorem is real, and so is the C matrix. I think they have used that v1 and v2 are conjugates, and so is lambda 1 and lambda 2.

How would you show this theorem? Can you use ordinary diagonolisation to show it?

 

[arkajad]

I would suggest: check that AP= PC writing A with some matrix elements (say p,q,r,s) and using the definitions.

 

[robotopia]

Before showing the theorem, I'll first establish the lemma that if you have two real 2x2 matrices, and if you multiply them on the right by $\begin{bmatrix} 1 \\ i \end{bmatrix}$ and you get the same result for both, then the two original matrices are the same:

Let $X= \begin{bmatrix} x_1 & x_2 \\ x_3 & x_4 \end{bmatrix}$ and $Y= \begin{bmatrix} y_1 & y_2 \\ y_3 & y_4 \end{bmatrix}$. Then if
$$\begin{align}X\begin{bmatrix} 1 \\ i \end{bmatrix} &= Y\begin{bmatrix} 1 \\ i \end{bmatrix}, \\ \begin{bmatrix} x_1 & x_2 \\ x_3 & x_4 \end{bmatrix}\begin{bmatrix} 1 \\ i \end{bmatrix} &= \begin{bmatrix} y_1 & y_2 \\ y_3 & y_4 \end{bmatrix}\begin{bmatrix} 1 \\ i \end{bmatrix} \end{align} \\ \begin{bmatrix} x_1 + x_2i \\ x_3 + x_4i \end{bmatrix} = \begin{bmatrix} y_1 + y_2i \\ y_3 + y_4i \end{bmatrix}$$
Hence $x_1=y_1$, $x_2=y_2$, $x_3=y_3$, $x_4=y_4$, and hence $X=Y$.

Now for the theorem itself:
Notice that $P \begin{bmatrix} 1 \\ i \end{bmatrix} = {\bf v}$ and that
$$C\begin{bmatrix} 1 \\ i \end{bmatrix}=\begin{bmatrix} a-bi \\ b+ai \end{bmatrix}=\begin{bmatrix} \lambda \\ \lambda i \end{bmatrix} = \lambda\begin{bmatrix} 1 \\ i \end{bmatrix}.$$
Then, for any real matrix $A$ with complex eigenvalues, we have
$$\begin{align}A{\bf v} &= \lambda {\bf v} \\ AP\begin{bmatrix} 1 \\ i \end{bmatrix} &= \lambda P\begin{bmatrix} 1 \\ i \end{bmatrix} \\ &= P \lambda \begin{bmatrix} 1 \\ i \end{bmatrix} \\ &= PC \begin{bmatrix} 1 \\ i \end{bmatrix}\end{align}$$
But both $AP$ and $PC$ are real, hence
$$AP=PC \quad \text{or} \quad A=PCP^{-1}.$$

 

[bobby2k]

Very nice proof!, thank you very much!

 

[blue_raver22]

Yes, it is possible to show this theorem using the standard method of diagonalizing a matrix. The key is to recognize that the complex eigenvalues and eigenvectors can still be represented in terms of real numbers, as you have mentioned with the conjugates. This allows us to use the same diagonalization process as we would for real eigenvalues and eigenvectors.

To show this, we can start with the equation AP = PD, where A is our original matrix, P is the matrix of eigenvectors, and D is the diagonal matrix with the eigenvalues on the diagonal. Since we are dealing with complex eigenvalues and eigenvectors, we can rewrite this equation as AP = PDC, where C is a diagonal matrix with the complex conjugates of the eigenvalues on the diagonal.

Next, we can multiply both sides by the inverse of P to get A = PDCP^-1. We can then use the fact that P^-1 = P* (the conjugate transpose of P) to rewrite this as A = PDCP*. This is where the fact that the eigenvectors and eigenvalues are conjugates comes into play. Since P is a real matrix, its conjugate transpose is simply its transpose. This means that P* = P^T, and we can rewrite the equation as A = PDCP^T.

Now, since P is a matrix of eigenvectors, its columns are linearly independent. This means that P^T is invertible, and we can multiply both sides by P^T to get AP^T = PDC. This can then be rewritten as AP^T = PD, which is the same as AP = PD since P^T is invertible.

Therefore, we have shown that for complex eigenvalues and eigenvectors, AP = PD still holds, and the standard method of diagonalizing a matrix can be used to prove this theorem.