annikaw
- 1
- 0
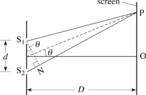
In a double-slit experiment, the distance between slits is 5.0mm and the slits are 1.0m from the screen. Two interference patterns can be seen on the screen: one due to light of wavelength 480nm, and the other due to light of wavelength 600nm. What is the separation on the screen between the third-order (m=3) bright fringes of the two interference patterns?
From my notes, I find that $d\sin\theta=m\lambda$.
However, I do not know how to get values of $\theta$ that can be put to the equation to find the difference in separation.
From my notes, I find that $d\sin\theta=m\lambda$.
However, I do not know how to get values of $\theta$ that can be put to the equation to find the difference in separation.
Last edited by a moderator: