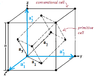
aaaa202
- 1,144
- 2
The interplanar spacing between planes labeled by miller indices (hkl) is given by:
d=2\pi/lGl
where G is the reciprocal lattice vector:
G=hb1+kb2+kb3
Somehow I can't get this formula to work. I wonna calculate the distance between (200) planes. This should be a/2, where a is the lattice constant. But (look it up) b1=2\pi/a (-x + y +z), where x, y and z are unit vectors. And so G= hb1 = 2\pi/a (-x + y +z) and thus lGl = h2\pi/a * √3
=>
d= a/(2√3)
But this can't be right. I have no idea why I get that factor of √3, because I checked everything. Where did I make a silly mistake?
d=2\pi/lGl
where G is the reciprocal lattice vector:
G=hb1+kb2+kb3
Somehow I can't get this formula to work. I wonna calculate the distance between (200) planes. This should be a/2, where a is the lattice constant. But (look it up) b1=2\pi/a (-x + y +z), where x, y and z are unit vectors. And so G= hb1 = 2\pi/a (-x + y +z) and thus lGl = h2\pi/a * √3
=>
d= a/(2√3)
But this can't be right. I have no idea why I get that factor of √3, because I checked everything. Where did I make a silly mistake?