- #1
Nile3
- 42
- 0
Hello, I was wondering if someone knew the equation which describe the exact or statistical relation between the length(# of digits) of a power of 2 based on it's power.
I plotted 200 of the powers in mathematica and I get a fairly straightforward staircase plot. I'm just wondering what's the rule here.
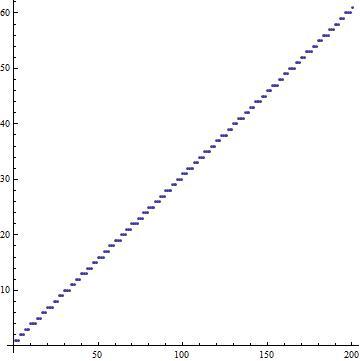
I plotted 200 of the powers in mathematica and I get a fairly straightforward staircase plot. I'm just wondering what's the rule here.