SUMMARY
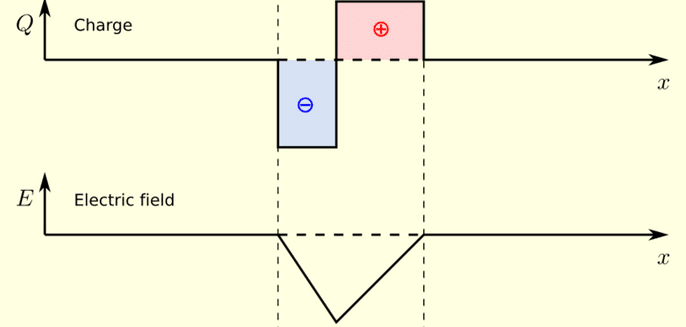
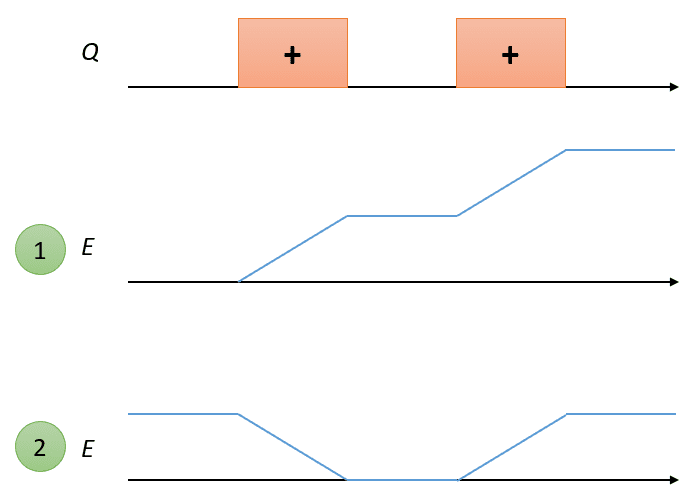
The discussion centers on the application of the 1D equation (dE/dx = λ/ε0) in analyzing electric fields between charge densities. It is established that when integrating charge density, a constant of integration must be added to account for boundary conditions, which can result in an electric field of zero between two charges. The participants clarify that the direction of the electric field on either side of the charges opposes each other, and this must be reflected in the graphical representation of the field. Misinterpretations of the equation's application are addressed, emphasizing the importance of correctly applying boundary conditions.
PREREQUISITES
- Understanding of electric field concepts
- Familiarity with charge density and its integration
- Knowledge of boundary conditions in physics
- Proficiency in interpreting graphical representations of electric fields
NEXT STEPS
- Study the implications of boundary conditions in electrostatics
- Learn about the integration of charge density in electric field calculations
- Explore graphical methods for representing electric fields
- Investigate the role of constants of integration in physics equations
USEFUL FOR
Students and professionals in physics, particularly those focusing on electrostatics, electrical engineering, and anyone interested in understanding electric field behavior in relation to charge distributions.