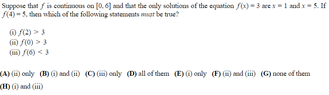Umar
- 36
- 0
View attachment 6010
Hi there, I'm having trouble with the above question. Basically, I need to determine which, or all of the statements are true. I've tried coming up with different ways the function can look like to satisfy or not satisfy the statements, but have come to no luck in doing so. If anyone could assist me on this one, that would be appreciated.
Hi there, I'm having trouble with the above question. Basically, I need to determine which, or all of the statements are true. I've tried coming up with different ways the function can look like to satisfy or not satisfy the statements, but have come to no luck in doing so. If anyone could assist me on this one, that would be appreciated.