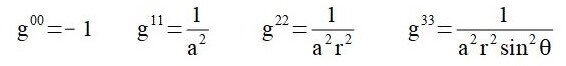Is the FLRW Metric a Valid Approximation for Our Universe on Large Scales?
- Context: Graduate
- Thread starter Tanujhm
- Start date
-
- Tags
- Metric
Click For Summary
The forum discussion centers on the validity of the Friedmann-Lemaître-Robertson-Walker (FLRW) metric as an approximation for our universe on large scales. Participants argue that while the FLRW metric is the only known exact solution to the Einstein field equations, it is only valid under conditions of perfect homogeneity and isotropy. The discussion highlights the mathematical implications of using the FLRW metric, particularly the violation of information conservation when deviations from these conditions are assumed. Key references include the work of Matthew Kleban and Leonardo Senatore, which challenges the applicability of the FLRW metric in real cosmological scenarios.
PREREQUISITES- Understanding of the Friedmann-Lemaître-Robertson-Walker (FLRW) metric
- Familiarity with Einstein's field equations
- Knowledge of cosmological principles and assumptions
- Basic grasp of mathematical concepts related to metric signatures
- Research the implications of the FLRW metric in cosmology
- Study the paper "Inhomogeneous and Anisotropic Cosmology" by Matthew Kleban and Leonardo Senatore
- Examine alternative cosmological models that challenge the FLRW approximation
- Explore the concept of information conservation in the context of general relativity
Cosmologists, theoretical physicists, and students of general relativity who are interested in the limitations of the FLRW metric and its implications for understanding the universe's structure and evolution.
Similar threads
- · Replies 6 ·
- · Replies 9 ·
- · Replies 27 ·
- · Replies 3 ·
- · Replies 13 ·
- · Replies 8 ·
- · Replies 24 ·
- · Replies 27 ·
- · Replies 8 ·
- · Replies 8 ·