Gwinterz
- 27
- 0
Hey, I have been stuck on this question for a while:
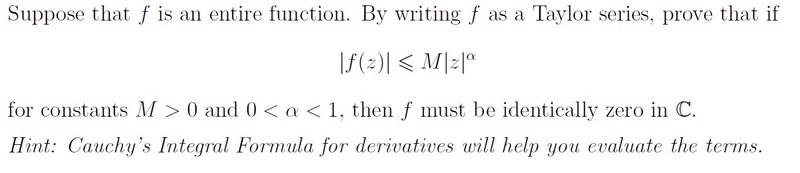
I have tried to follow the hint, but I am not sure where to go next to get the result.

Have I started correctly? I am not sure how to show that the integral is zero.
If I can show it is less than zero, I also don't see how that shows it is always zero.
Thanks in advance for any help.
I have tried to follow the hint, but I am not sure where to go next to get the result.

Have I started correctly? I am not sure how to show that the integral is zero.
If I can show it is less than zero, I also don't see how that shows it is always zero.
Thanks in advance for any help.