Feynstein100
- 181
- 17
So I ran a python simulation of 1,000 games of toss (50/50 odds) where each game consists of 100,000 consecutive flips. The result was this:
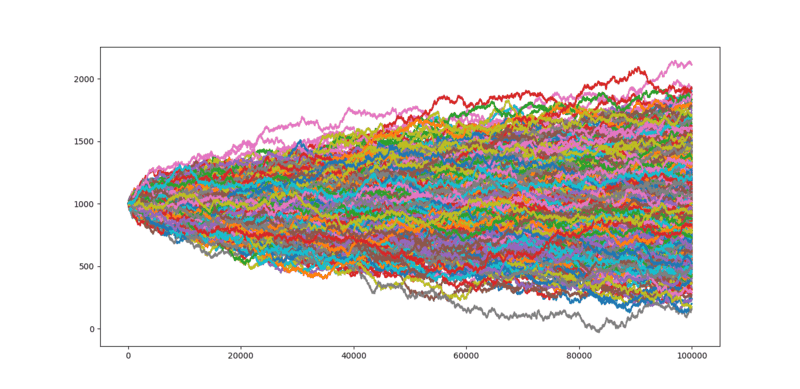
1000 is our starting balance and as expected, there's a nice normal distribution around it. I also calculated the average value after all the games and it was around 1000, again, as expected.
However, then it occurred to me that the expected profit/loss is zero because our graph here represents all possibilities (almost but it's a representative sample so bear with me) and the graph is symmetric about the starting balance i.e. there are just as many outcomes above the starting value as there are under it. Hence, on average, there's no gain/loss.
So I thought, what if that weren't true? What if we made the graph asymmetric? If we quit once we reached a balance of, say, 980, the graph would look something like this:
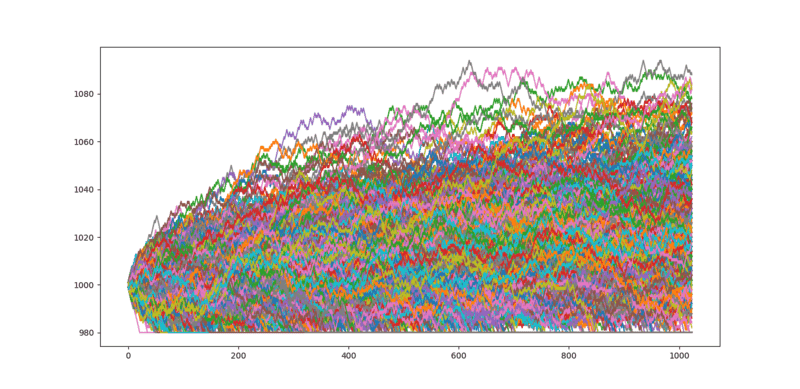
Idk if you guys are familiar with daytrading terms but in case you aren't, this is called a stop-loss, i.e. a thing that prevents you from losing more money than the level you set it at. Anyway, since this graph is clearly asymmetric, I expected more outcomes to be above 1000 than below it. This should've led to a clear profit over the long run. And yet, even when I did 100,000 flips with the stop loss, the average outcome was still around 1000. I'm at a loss as to why that happened. From a purely geometrical point of view, there should've been a net profit.
The graph seems to be following a y = sqrt(x) curve both above and below the starting balance. I assumed the profit/loss would simply be the area under the curves. Profit for the part above 1000 and loss for the part below 1000. Without the stop-loss, these two areas would be equal and cancel each other out, thus no net profit/loss. But with the lower area now restricted because of the stop loss, shouldn't there be more area above and hence a profit? What am I missing here? Is it perhaps incorrect to calculate profit/loss this way?
1000 is our starting balance and as expected, there's a nice normal distribution around it. I also calculated the average value after all the games and it was around 1000, again, as expected.
However, then it occurred to me that the expected profit/loss is zero because our graph here represents all possibilities (almost but it's a representative sample so bear with me) and the graph is symmetric about the starting balance i.e. there are just as many outcomes above the starting value as there are under it. Hence, on average, there's no gain/loss.
So I thought, what if that weren't true? What if we made the graph asymmetric? If we quit once we reached a balance of, say, 980, the graph would look something like this:
Idk if you guys are familiar with daytrading terms but in case you aren't, this is called a stop-loss, i.e. a thing that prevents you from losing more money than the level you set it at. Anyway, since this graph is clearly asymmetric, I expected more outcomes to be above 1000 than below it. This should've led to a clear profit over the long run. And yet, even when I did 100,000 flips with the stop loss, the average outcome was still around 1000. I'm at a loss as to why that happened. From a purely geometrical point of view, there should've been a net profit.
The graph seems to be following a y = sqrt(x) curve both above and below the starting balance. I assumed the profit/loss would simply be the area under the curves. Profit for the part above 1000 and loss for the part below 1000. Without the stop-loss, these two areas would be equal and cancel each other out, thus no net profit/loss. But with the lower area now restricted because of the stop loss, shouldn't there be more area above and hence a profit? What am I missing here? Is it perhaps incorrect to calculate profit/loss this way?