Is this a valid derivation of the Uncertainty Principle?

[patric44]

Homework Statement:: i saw this simple derivation of the uncertainty principle in my college introductory quantum book
Relevant Equations:: Δp.Δx = h

hi guys
i saw this derivation of the uncertainty principle in my college quantum book , but the derivation seems very simple and sloppy , i mean the i saw multiple derivations of the uncertainty principle using Fourier analysis and Schwarz inequality and so on , so this derivation seems so simple to be true ?!
the derivation goes like this :

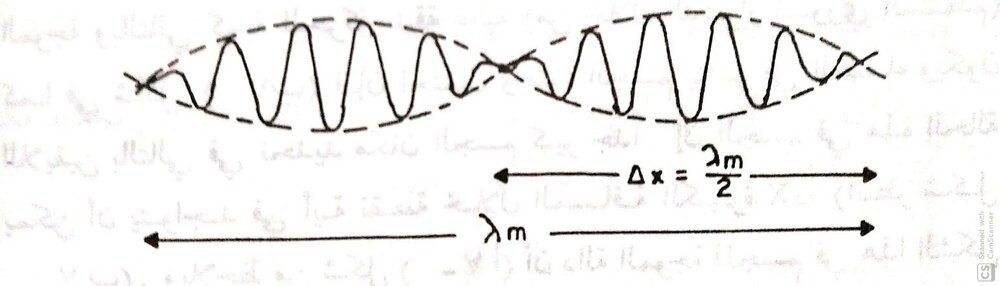
assume that the wave function of the particle is given by this figure , then the uncertainty of the position
$$Δx = \frac{λ_{m}}{2}$$
this can be written as :
$$λ_{m} = \frac{2\pi}{\frac{1}{2}Δk} ⇒$$
$$Δx = \frac{2\pi}{Δk}$$
and since
$$k = \frac{2\pi}{h}p ⇒ Δk = \frac{2\pi}{h}Δp ⇒ Δp = \frac{h}{2\pi}Δk $$
and so :
$$ΔxΔp = h$$

my objection is that the derivation seems very simple , and that the wave function itself don't describe the position of the particle as it was stated ?! so is this a valid but rather crude derivation of the uncertainty principle or its a nonsense ! and why .

 

[PeroK]

It's not so much valid as perhaps a way to convince yourself that QM is not totally unreasonable.

There's an excellent analysis of how you can develop these quantum ideas and how to put them in the correct context here:

https://physics.mq.edu.au/~jcresser/Phys304/Handouts/QuantumPhysicsNotes.pdf

 

[patric44]

thank you so much these notes seems awesome

 

[Israel Medina]

The problem is that the meaning of the principle you already included in your assumptions when you set :
\Delta x = \frac{\lambda}{2}.
From there you can do whatever you want. Take a look to the Sakurai and check the obtaining of the principle from scratch