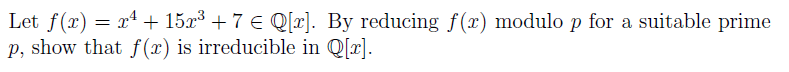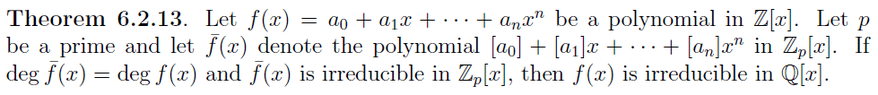Is x^4+x^3+1 Irreducible in Q[x] and Z[x]?

  • Context: MHB 
  • Thread starter Thread starter Joe20
  • Start date Start date
Click For Summary
SUMMARY

The polynomial \(x^4+x^3+1\) is confirmed to be irreducible over both \(\mathbb{Q}[x]\) and \(\mathbb{Z}[x]\). The only candidate for a quadratic divisor is \(x^2+x+1\), which was tested against the polynomial. The calculation shows that \((x^2+x+1)^2\) results in \(x^4+x^2+1\), which does not equal \(x^4+x^3+1\). Therefore, no factorization exists, establishing the irreducibility of the polynomial.

PREREQUISITES
  • Understanding of polynomial factorization
  • Familiarity with irreducibility criteria in algebra
  • Knowledge of quadratic polynomials
  • Basic proficiency in algebraic manipulation
NEXT STEPS
  • Study the irreducibility of polynomials in \(\mathbb{Q}[x]\) and \(\mathbb{Z}[x]\)
  • Learn about the properties of quadratic polynomials and their role in factorization
  • Explore polynomial long division techniques
  • Investigate other irreducible polynomials and their applications in algebra
USEFUL FOR

Mathematicians, algebra students, and educators interested in polynomial theory and irreducibility concepts.

Joe20
Messages
53
Reaction score
1
Hi all, appreciate your help to look through my answers to see if they are correct.

Thank you.
 

Attachments

  • q2.png
    q2.png
    5.5 KB · Views: 98
  • Webp.net-resizeimage.q2.jpg
    Webp.net-resizeimage.q2.jpg
    131.2 KB · Views: 94
  • T.png
    T.png
    10.3 KB · Views: 97
Physics news on Phys.org
Looks good to me. If you wanted to avoid the long division, you could observe that the only candidate for a quadratic divisor of $\overline{f}(x)$ is $x^2+x+1$ (since you have already ruled out the other three quadratic polynomials). So the only possible factorisation would be if $x^4+x^3 + 1 = (x^2+x+1)^2$. But $(x^2+x+1)^2 = x^4+x^2 + 1 \ne x^4+x^3 + 1$. It follows that $x^4+x^3 + 1$ is irreducible.
 

Similar threads

Undergrad How to show ##p(x)=g(x)x\pm 1\in\Bbb{Q}[x]## is irreducible in ##\Bbb{Q}_{\Bbb{Z}}[x]##?
  • · Replies 48 ·
2
Replies
48
Views
5K
MHB The polynomial is irreducible over Q(i)
  • · Replies 16 ·
Replies
16
Views
4K
MHB Proving Z[x] and Q[x] is not isomorphic
  • · Replies 5 ·
Replies
5
Views
3K
Undergrad Proof for subgroup -- How prove it is a subgroup of Z^m?
  • · Replies 11 ·
Replies
11
Views
3K
MHB Irreducible Polynomial g = X^4 + X + 1 over F2
  • · Replies 3 ·
Replies
3
Views
2K
Undergrad Variant of Baker-Campbell-Hausdorff Formula
  • · Replies 3 ·
Replies
3
Views
2K
MHB Prove the polynomial f(x)=x^2-q is irreducible in F_p[x]?
  • · Replies 1 ·
Replies
1
Views
2K
Undergrad Localizing single variable quotient polynomial ring at a prime ideal
  • · Replies 6 ·
Replies
6
Views
1K
Undergrad Did I figure-out z-translation of 2D-coordinates correctly?
  • · Replies 4 ·
Replies
4
Views
3K
MHB Basic Theory of Field Extensions - Exercise from D&F ....
  • · Replies 2 ·
Replies
2
Views
2K