MHB Jimmy Mai's ODEs Questions at Yahoo Answers

[MarkFL]

Here are the questions:

Differential Equation 3.6?

Express the solution of the given initial value problem as a sum of 2 oscillations. Throughout, primes denote derivatives with respect to time t. Graph the solution function x(t) in such a way that you can identify its period.

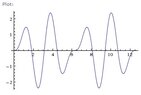
2. x"+4x=5sin3t x(0)=x'(0)=0

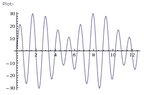
4. x"+25x=90cos4t x(0)=0 x'(0)=90

Answer is x(t)=3/2 sin2t-sin3t and

x(t)=2√(106) cos(5t-alpha) + 10cos4t with alpha=pi-inverse tan(9/5) = 2.0779

I have no idea how to do this type of problem. Thank you for your help.

I have posted a link there to this topic so the OP can see my work.

 

[MarkFL]

Hello Jimmy Mai,

2.) We are given the IVP:

$$x"+4x=5\sin(3t)$$ where $$x(0)=x'(0)=0$$

The first thing we want to do is find the associated homogeneous solution $$x_h(t)$$. We see that the characteristic equation is:

$$r^2+4=0$$

Thus, the characteristic roots are:

$$r=\pm2i$$

and so we may state:

$$x_h(t)=c_1\cos(2t)+c_2\sin(2t)$$

We may choose, using a linear combination identity, to write this solution as:

$$x_h(t)=c_1\sin\left(2t+c_2 \right)$$

Now, using the method of undetermined coefficients, we may look for a particular solution $$x_p(t)$$ of the form:

$$x_p(t)=A\sin(3t+B)$$

Differentiating twice with respect to $t$, we find:

$$x_p''(t)=-9A\sin(3t+B)$$

Substituting the particular solution into the original ODE, we may now determine the parameters $A$ and $B$:

$$\left(-9A\sin(3t+B) \right)+4\left(A\sin(3t+B) \right)=5\sin(3t)$$

$$-5A\sin(3t+B)=5\sin(3t+0)$$

Hence, we see that:

$$A=-1,\,B=0$$

and so:

$$x_p(t)=-\sin(3t)$$

By superposition, we may state the general solution to the ODE as:

$$x(t)=x_h(t)+x_p(t)=c_1\sin\left(2t+c_2 \right)-\sin(3t)$$

Now, to determine the solution satisfying the initial values, we need to differentiate the general solution with respect to $t$ to obtain:

$$x'(t)=2c_1\cos\left(2t+c_2 \right)-3\cos(3t)$$

Now we may write:

$$x(0)=c_1\sin\left(c_2 \right)=0$$

$$x'(0)=2c_1\cos\left(c_2 \right)-3=0$$

From these equations, we may observe that $c_1\ne0$, and so we have:

$$c_1=\frac{3}{2},\,c_2=0$$

Thus, the solution satisfying the IVP is:

$$x(t)=\frac{3}{2}\sin(2t)-\sin(3t)$$

A plot of the solution shows its period is $T=2\pi$:

View attachment 907

 

[MarkFL]

4.) We are given the IVP:

$$x"+25x=90\cos(4t)$$ where $$x(0)=0,\,x'(0)=90$$

As before, we first want to find $x_h(t)$. We see the associated characteristic equation is:

$$r^2+5=0$$

and so:

$$r=\pm5i$$

Thus, the homogeneous solution may be written:

$$x_h(t)=c_1\cos\left(5t+c_2 \right)$$

Next, we may use undetermined coefficients to find a particular solution of the form:

$$x_p(t)=A\cos(4t+B)$$

Differentiating twice with respect to $t$, we find:

$$x_p''(t)=-16A\cos(4t+B)$$

Substituting into the original ODE, we find:

$$\left(-16A\cos(4t+B) \right)+25\left(A\cos(4t+B) \right)=90\cos(4t)$$

$$9A\cos(4t+B)=90\cos(4t+0)$$

From this we determine:

$$A=10,\,B=0$$

and so we have:

$$x_p(t)=10\cos(4t)$$

By superposition, we may the give the general solution to the ODE as:

$$x(t)=x_h(t)+x_p(t)=c_1\cos\left(5t+c_2 \right)+10\cos(4t)$$

Now, to determine the solution satisfying the initial values, we need to differentiate the general solution with respect to $t$ to obtain:

$$x'(t)=-5c_1\sin\left(5t+c_2 \right)-40\sin(4t)$$

Now we may write:

$$x(0)=c_1\cos\left(c_2 \right)+10=0$$

$$x'(0)=-5c_1\sin\left(c_2 \right)=90$$

Solving both for $c_1$, we find:

$$c_1=-\frac{10}{\cos\left(c_2 \right)}=-\frac{18}{\sin\left(c_2 \right)}$$

$$5\sin\left(c_2 \right)=9\cos\left(c_2 \right)$$

$$\tan\left(c_2 \right)=\frac{9}{5}$$

$$c_2=\tan^{-1}\left(\frac{9}{5} \right)$$

$$c_1=-\frac{10}{\cos\left(\tan^{-1}\left(\frac{9}{5} \right) \right)}=-2\sqrt{106}$$

Thus we may state the solution satisfying the given IVP is:

$$x(t)=-2\sqrt{106}\cos\left(5t+\tan^{-1}\left(\frac{9}{5} \right) \right)+10\cos(4t)$$

Using the identity $$\cos(\theta-\pi)=-\cos(\theta)$$, we may write this solution as:

$$x(t)=2\sqrt{106}\cos\left(5t-\left(\pi-\tan^{-1}\left(\frac{9}{5} \right) \right) \right)+10\cos(4t)$$

A plot of the solution shows its period is $T=2\pi$:

View attachment 908