MHB Joey e's questions at Yahoo Answers regarding solids of revolution

[MarkFL]

Here is the question:

Calculus Disc/washer/shell method.?

I have two problems that I have no idea how to work, and have the test coming up soon.

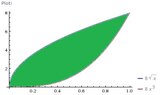
1) Sketch the region by the following curves and find the volume of the solid generated by revolving this region about the x-axis.

y=8sqrtx
y=8x^3

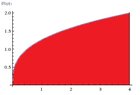
2) Sketch the region bounded by the following curves and find the volume of the solid generated by the revolving this region about the y-axis.

x=1/2y^3
x=4
y=0

I need to know why you picked the method you did, and the work shown associated with it. THANK YOU SO MUCH

Here is a link to the questions:

Calculus Disc/washer/shell method.? - Yahoo! Answers

I have posted a link there to this topic so the OP can find my response.

 

[MarkFL]

Re: joey e's questions from Yahoo! Answers regarding solids of revolution

Hello joey e,

I am going to work both problems using the disk/washer method and the shell method so you can see both in action and as a means of checking my work, plus it's good practice when practical.

1.) Let's first look at a plot of the region to be revolved about the $x$-axis:

https://www.physicsforums.com/attachments/780._xfImport

Washer method:

Let's find the volume $dV$ of an arbitrary washer:

$$dV=\pi\left(R^2-r^2 \right)\,dx$$

$R$ is the outer radius, and it is given by:

$$R=8\sqrt{x}$$

$r$ is the inner radius, and it is given by:

$$r=8x^3$$

and so we have:

$$dV=64\pi\left(x-x^6 \right)\,dx$$

Summing the washers by integrating, we find:

$$V=64\pi\int_0^1 x-x^6\,dx=64\pi\left[\frac{x^2}{2}-\frac{x^7}{7} \right]_0^1=64\pi\left(\frac{1}{2}-\frac{1}{7} \right)=\frac{160\pi}{7}$$

Shell method:

The volume $dV$ of an arbitrary shell is:

$$dV=2\pi rh\,dy$$

where:

$$r=y$$

$$h=\frac{y^{\frac{1}{3}}}{2}-\frac{y^2}{64}$$

and so we have:

$$dV=\pi \left(y^{\frac{4}{3}}-\frac{y^3}{32} \right)\,dy$$

Summing the shells by integrating, we find:

$$V=\pi\int_0^8 y^{\frac{4}{3}}-\frac{y^3}{32}\,dy=\pi\left[\frac{3}{7}y^{\frac{7}{3}}-\frac{1}{128}y^4 \right]_0^8=\pi\left(\frac{3}{7}8^{\frac{7}{3}}-\frac{1}{128}8^4 \right)=\frac{160\pi}{7}$$

2.) Here is a plot of the region to be revolved about the $y$-axis:

https://www.physicsforums.com/attachments/781._xfImport

Washer method:

The volume $dV$ of an arbitrary washer is:

$$dV=\pi\left(R^2-r^2 \right)\,dy$$

$$R=4$$

$$r=\frac{1}{2}y^3$$

and so we have:

$$dV=\pi\left(16-\frac{1}{4}y^6 \right)\,dy$$

Summing the washers by integrating, we find:

$$V=\pi\int_0^2 16-\frac{1}{4}y^6\,dy=\pi\left[16y-\frac{1}{28}y^7 \right]_0^2=\pi\left(16\cdot7-\frac{1}{28}2^7 \right)=\frac{192\pi}{7}$$

Shell method:

The volume $dV$ of an arbitrary shell is:

$$dV=2\pi rh\,dx$$

$$r=x$$

$$h=(2x)^{\frac{1}{3}}$$

and so we have:

$$dV=2^{\frac{4}{3}}\pi x^{\frac{4}{3}}\,dx$$

Summing the shells by integration, we find:

$$V=2^{\frac{4}{3}}\pi\int_0^4 x^{\frac{4}{3}}\,dx=2^{\frac{4}{3}}\pi\left[\frac{3}{7}x^{\frac{7}{3}} \right]_0^4=2^{\frac{4}{3}}\pi\cdot\frac{3}{7}4^{\frac{7}{3}}=\frac{192\pi}{7}$$

To joey e and any other guests viewing this topic, I invite and encourage you to post other solids of revolution problems here in our http://www.mathhelpboards.com/f10/ forum.

Best Regards,

Mark.